题目内容
计算或化简(1)(2
 -
- )×
)×
(2)
 (a>0,b>0)
(a>0,b>0)(3)计算:

(4)若
 ,先化简再求
,先化简再求 的值.
的值.
【答案】分析:(1)首先将二次根式化简,再去括号相乘即可得出答案;
(2)首先二次根式除法化成乘法,再将根号外的相乘,根号内的相乘,化简即可;
(3)利用二次根式的化简,将分母有理化,再通分即可,
(4)根据 <0,即二次根式化简,再代入求值即可.
<0,即二次根式化简,再代入求值即可.
解答:解:(1)(2 -
-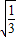 )×
)×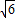 ,
,
=(4 -3×
-3×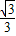 )×
)×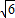 ,
,
=3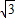 ×
× ,
,
=9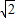 ;
;
(2) (a>0,b>0),
(a>0,b>0),
=
 •
•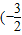
 )×
)×
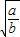 ,
,
=[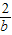 ×(-
×(- )×
)× ]×
]× ,
,
=(-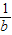 )
)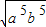 ,
,
=-a2b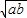 ;
;
(3)计算: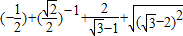 ,
,
=1+ +
+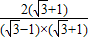 +2-
+2- ,
,
=1+ +
+ +1+2-
+1+2-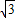 ,
,
=4+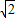 ;
;
(4)∵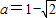 <0,
<0,
∴ ,
,
= +
+ ,
,
=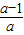 +
+ ,
,
= ,
,
∵ ,
,
∴原式= =
=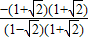 =3+2
=3+2 .
.
点评:此题主要考查了二次根式的化简求值以及二次根式的混和运算等知识,在二次根式的混合运算中,能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径是解题关键.
(2)首先二次根式除法化成乘法,再将根号外的相乘,根号内的相乘,化简即可;
(3)利用二次根式的化简,将分母有理化,再通分即可,
(4)根据
 <0,即二次根式化简,再代入求值即可.
<0,即二次根式化简,再代入求值即可.解答:解:(1)(2
 -
-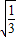 )×
)×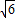 ,
,=(4
 -3×
-3×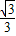 )×
)×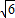 ,
,=3
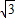 ×
× ,
,=9
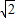 ;
;(2)
 (a>0,b>0),
(a>0,b>0),=

 •
•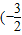
 )×
)×
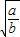 ,
,=[
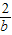 ×(-
×(- )×
)× ]×
]× ,
,=(-
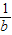 )
)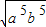 ,
,=-a2b
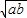 ;
;(3)计算:
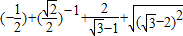 ,
,=1+
 +
+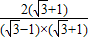 +2-
+2- ,
,=1+
 +
+ +1+2-
+1+2-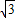 ,
,=4+
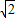 ;
;(4)∵
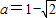 <0,
<0,∴
 ,
,=
 +
+ ,
,=
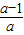 +
+ ,
,=
 ,
,∵
 ,
,∴原式=
 =
=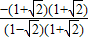 =3+2
=3+2 .
.点评:此题主要考查了二次根式的化简求值以及二次根式的混和运算等知识,在二次根式的混合运算中,能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径是解题关键.

练习册系列答案
相关题目