题目内容
【题目】某水果基地积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
【答案】(1)装运乙种水果的车有2辆、丙种水果的汽车有6辆;(2)装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆;(3)当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366元.
【解析】试题分析:(1)根据“8辆汽车装运乙、丙两种水果共22吨到A地销售”列出方程组,即可解答;
(2)设装运乙、丙水果的车分别为a辆,b辆,列出方程组,即可解答;
(3)设总利润为w千元,表示出w=10m+216.列出不等式组,确定m的取值范围13≤m≤15.5,结合一次函数的性质,即可解答.
试题解析:(1)设装运乙、丙水果的车分别为x辆,y辆,得: ![]() ,解得:
,解得: ![]() .
.
答:装运乙种水果的车有2辆、丙种水果的汽车有6辆.
(2)设装运乙、丙水果的车分别为a辆,b辆,得: ![]() ,解得:
,解得: ![]() .
.
答:装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆.
(3)设总利润为w千元,w=4×5m+2×7(m﹣12)=4×3(32﹣2m)=10m+216.
∵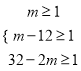 ,∴13≤m≤15.5,∵m为正整数,∴m=13,14,15,在w=10m+216中,w随x的增大而增大,∴当m=15时,W最大=366(千元).
,∴13≤m≤15.5,∵m为正整数,∴m=13,14,15,在w=10m+216中,w随x的增大而增大,∴当m=15时,W最大=366(千元).
答:当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366元.