Question

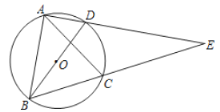
【题目】如图，BD是⊙O的直径， A、C是⊙O上的两点，且AB=AC，AD与BC的延长线交于点E．

（1）求证：△ABD∽△AEB；

（2）若AD=1，DE=3，求BD的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）结合已知条件就可以推出∠ABC=∠ADB，再加上公共角就可以推出结论；

（2）由（1）的结论就可以推出AB的长度，规矩勾股定理即可推出BD的长度．

解：（1）证明：∵AB=AC

∴

∴∠ABC=∠ADB

又∠BAE=∠DAB，

∴△ABD∽△AEB．

（2）解：∵△ABD∽△AEB，

∴

∵ AD=1，DE=3，

∴AE=4.

∴ AB2=AD·AE=1×4=4.

∴ AB=2

∵ BD是⊙O的直径，

∴∠DAB=90°

在Rt△ABD中，BD2=AB2＋AD2=22＋12=5，

∴BD=．