题目内容
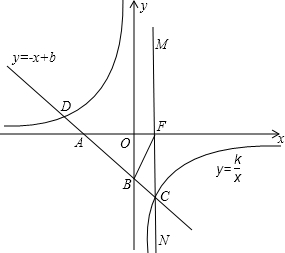 直线y=-x+b与双曲线y=
直线y=-x+b与双曲线y=| k | x |
(1)求直线和双曲线的解析式;
(2)求∠BCF的度数;
(3)设直线MN上有一动点P,过P作直线PE⊥AB,垂足为E,直线PE与x轴相交于点H.当P点在直线MN上移动时,是否存在这样的P点,使以A、P、H为顶点的三角形与△FBC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
分析:(1)直接把点D(-4,1)代入直线y=-x+b与双曲线y=
即可得出结论;
(2)根据反比例函数的解析式易求点C的坐标,则由A、C的坐标可以求得∠BCF=45°;
(3)从图中不难看出∠AHP、∠ACF是同角(或等角)的余角,那么必有∠AHP=∠FCB=45°,首先用未知数设出PF的长,进而由∠AHP的度数求出PH、AH的长,若△AHP、△FCB相似,通过得到的比例线段列式求出这个未知数的值,由此确定点P的坐标(注意要分点P在x轴上方和下方两种情况讨论).
| k |
| x |
(2)根据反比例函数的解析式易求点C的坐标,则由A、C的坐标可以求得∠BCF=45°;
(3)从图中不难看出∠AHP、∠ACF是同角(或等角)的余角,那么必有∠AHP=∠FCB=45°,首先用未知数设出PF的长,进而由∠AHP的度数求出PH、AH的长,若△AHP、△FCB相似,通过得到的比例线段列式求出这个未知数的值,由此确定点P的坐标(注意要分点P在x轴上方和下方两种情况讨论).
解答: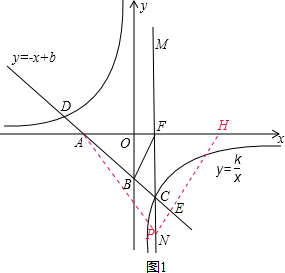 解:(1)∵直线y=-x+b与双曲线y=
解:(1)∵直线y=-x+b与双曲线y=
相交于点D(-4,1),
∴1=4+b,解得b=-3;
1=
,解得k=-4.
∴直线解析式为y=-x-3,双曲线解析式为y=-
;
(2)∵点C(1,m)在反比例函数y=-
上,
∴m=-
=-4,
∴C(1,-4).
由点A(-3,0)、C(1,-4)得:AF=CF=4,即△AFC是等腰直角三角形,∠BCF=45°;
(3)①如图1,当点P在x轴下方时,∠AHP=∠FCB=90°-∠HAC=45°;
 在Rt△FPH中,设FH=FP=x,则PH=
在Rt△FPH中,设FH=FP=x,则PH=
x,AH=AF+FH=4+x;
由B(0,-3)、C(1,-4)知:BC=
,CF=4;
若△APH∽△HBC,那么
=
,则有:
=
,
解得:x=
,即 P(1,-
);
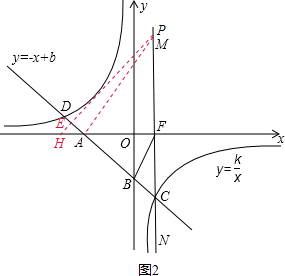
②如图2,当点P在x轴上方时,∠AHP=∠FCB=90°-∠EAH=90°-∠FAC=45°;
设FP=x,则 FH=FP=x,AH=FH-AF=x-4,PH=
x;
同1可得:
=
,有:
=
,
解得:x=8,即 P(1,8);
综上,点P的坐标为(1,-
)或(1,8).
 解:(1)∵直线y=-x+b与双曲线y=
解:(1)∵直线y=-x+b与双曲线y=| k |
| x |
∴1=4+b,解得b=-3;
1=
| k |
| -4 |
∴直线解析式为y=-x-3,双曲线解析式为y=-
| 4 |
| x |
(2)∵点C(1,m)在反比例函数y=-
| 4 |
| x |
∴m=-
| 4 |
| 1 |
∴C(1,-4).
由点A(-3,0)、C(1,-4)得:AF=CF=4,即△AFC是等腰直角三角形,∠BCF=45°;
(3)①如图1,当点P在x轴下方时,∠AHP=∠FCB=90°-∠HAC=45°;
 在Rt△FPH中,设FH=FP=x,则PH=
在Rt△FPH中,设FH=FP=x,则PH=| 2 |
由B(0,-3)、C(1,-4)知:BC=
| 2 |
若△APH∽△HBC,那么
| PH |
| BC |
| AH |
| CF |
| ||
|
| 4+x |
| 4 |
解得:x=
| 4 |
| 3 |
| 4 |
| 3 |
②如图2,当点P在x轴上方时,∠AHP=∠FCB=90°-∠EAH=90°-∠FAC=45°;
设FP=x,则 FH=FP=x,AH=FH-AF=x-4,PH=
| 2 |
同1可得:
| PH |
| CF |
| AH |
| BC |
| ||
| 4 |
| x-4 | ||
|
解得:x=8,即 P(1,8);
综上,点P的坐标为(1,-
| 4 |
| 3 |
点评:此题主要考查了函数解析式的确定、相似三角形的判定和性质等相关知识点;(2)较难,能够应用含有特殊度数的∠BCF是解答题目的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
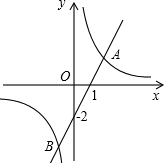 已知直线y=2x-2与双曲线图
已知直线y=2x-2与双曲线图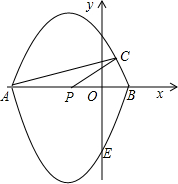 点,且P(-1,0),C(
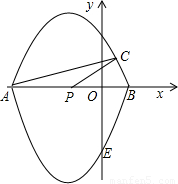
点,且P(-1,0),C(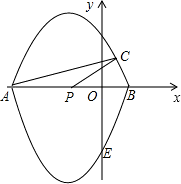 如图,在平面直角坐标系xOy中,经过点A,C,B的抛物线的一部分与经过点A,E,B的抛物线的一部分组合成一条封闭曲线,我们把这条封闭曲线称为“双抛物线”.已知P为AB中点,且P(-1,0),C(
如图,在平面直角坐标系xOy中,经过点A,C,B的抛物线的一部分与经过点A,E,B的抛物线的一部分组合成一条封闭曲线,我们把这条封闭曲线称为“双抛物线”.已知P为AB中点,且P(-1,0),C( -1,1),E(0,-3),S△CPA=1.
-1,1),E(0,-3),S△CPA=1.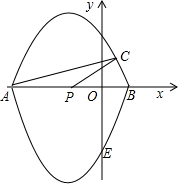 点,且P(-1,0),C(
点,且P(-1,0),C(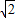 -1,1),E(0,-3),S△CPA=1.
-1,1),E(0,-3),S△CPA=1.