Question

【题目】如图，小浩从二次函数y=ax2+bx+c（a≠0）的图象中得到如下信息：
①ab＜0
②4a+b=0
③当y=5时只能得x=0
④关于x的一元二次方程ax2+bx+c=10有两个不相等的实数根，
你认为其中正确的有（ ）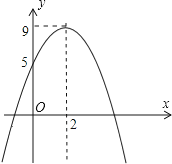

A.1个
B.2个
C.3个
D.4个

Answer 1

【答案】B
【解析】解：∵抛物线开口向下，
∴a＜0，
∵抛物线的对称轴为直线x=﹣ =2，
∴b=﹣4a，
∴b＞0，b+4a=0，所以①②正确；
∵抛物线的对称轴为直线x=2，
∴（0，5）和（4，5）是抛物线上两对称点，
∴x=0或4时，y=5，所以③错误；
∵抛物线的顶点坐标为（2，9），
∴y的最大值为9，
∴ax2+bx+c≤9，
∴一元二次方程ax2+bx+c=10无实数解，所以④错误．
故选B．
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）即可以解答此题．