题目内容
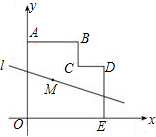如图，多边形OABCDE在平面直角坐标系中，O为坐标原点，点A和点E分别在y轴和x轴上，其中AB∥CD∥x轴，DE∥BC∥y轴，已知点B（4，6），点D（6，4），若直线l经过点M（2，3），且将多边形OABCDE分割成面积相等的两部分，则直线l的函数表达式是分析：设直线1为：y=kx+b．根据A、B、C、D、E坐标可先求出多边形面积，然后用k，b表示梯形的面积，由梯形面积是多边形面积的一半，再代入M的坐标，求出k，b．
解答：
解：如图所示，设直线1函数表达式为：y=kx+b．其中，点A和点E分别在y轴和x轴上，其中AB∥CD∥x轴，DE∥BC∥y轴，已知点B（4，6），点D（6，4），所以A（0，6），C（4，4），E（6，0）．
直线1与多边形交点坐标为：G（0，b），H（6，6k+b）．
多边形ABCDEO面积：S=8+16+8=32．
梯形HEOG面积为：m=6（3k+b）=0.5S=16．
将M（2，3）代入直线1：3=2k+b．
列出方程组：
解得：
所以直线1的方程表达式为：y=-
x+
．
解：如图所示，设直线1函数表达式为：y=kx+b．其中，点A和点E分别在y轴和x轴上，其中AB∥CD∥x轴，DE∥BC∥y轴，已知点B（4，6），点D（6，4），所以A（0，6），C（4，4），E（6，0）．直线1与多边形交点坐标为：G（0，b），H（6，6k+b）．
多边形ABCDEO面积：S=8+16+8=32．
梯形HEOG面积为：m=6（3k+b）=0.5S=16．
将M（2，3）代入直线1：3=2k+b．
列出方程组：
|
解得：
|
所以直线1的方程表达式为：y=-
| 1 |
| 3 |
| 11 |
| 3 |
点评：本题可以看成一个二元一次方程组，关键要找好等量关系，同时还应注意梯形面积的求法．
练习册系列答案
相关题目
A点运动，E为AB上一动点，点E以1cm/s的速度从A点出发向点B运动．
A点运动，E为AB上一动点，点E以1cm/s的速度从A点出发向点B运动．