Question

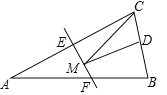
【题目】如图，等腰的底边长为4，面积为12，腰的垂直平分线分别交边于点，若点D是的中点，点M为线段上一动点，当的周长最小时，长为（ ）

A.1B.3C.D.

Answer 1

【答案】C

【解析】

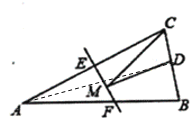
连接AD，由△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论.

连接AD，

∵△ABC是等腰三角形，点D是BC边的中点，

∴AD⊥BC，
∴,

解得AD=6，
∵EF是线段AC的垂直平分线，

∴AD的长为CM+MD的最小值，

己知AD⊥BC，即MD⊥BC，
在Rt△CDM中
设AM=x，则MC=x，MD=(6-x)，

∵CD2+MD2=MC2，
∴22+(6-x)2=x2，
解得x=即AM=,
∵AC=，
∴AE=，

∴EM==,

故选：C.