题目内容
【题目】若一个三角形的三个顶点均在一个图形的不同的边上，则称此三角形为该图形的内接三角形．
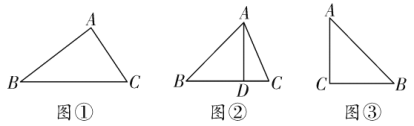
（1）在图①中画出△ABC的一个内接直角三角形；
（2）如图②，已知△ABC中，∠BAC＝60°，∠B＝45°，AB＝8，AD为BC边上的高，探究以D为一个顶点作△ABC的内接三角形，其周长是否存在最小值？若存在，请求出最小值；若不存在，请说明理由；
（3）如图③，△ABC为等腰直角三角形，∠C＝90°，AC＝６，试探究：△ABC的内接等腰直角三角形的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．
【答案】（1）见解析（2）存在，（3）
【解析】
试题分析：（1）根据要求画图即可，体现内接的特点；
（2）如解图②，分别作点D关于AB、AC的轴对称点
、
，连接
，交AB、AC于点E、F，
连接DE、DF，则△DEF即为周长最小的内接三角形，然后过点A作AH⊥EF于点H，根据对称性求解即可；
（3）分两种情况讨论：①当内接等腰直角三角形的直角顶点在斜边AB上时；②当内接等腰直角三角形的直角顶点在直角边上时．
试题解析：（1）如解图①，△DEF为所求作的三角形（答案不唯一）；
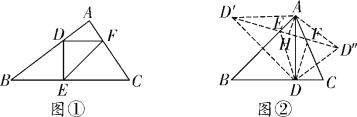
（2）存在．
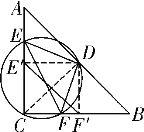
如解图②，分别作点D关于AB、AC的轴对称点
、
，连接
，交AB、AC于点E、F，
连接DE、DF，则△DEF即为周长最小的内接三角形，
的长即为最小周长．
∵AB＝８，∠Ｂ＝45°，AD⊥BC，∴AD＝AB·si45°＝
．
∵点D关于AB、AC的轴对称点分别为
、
，
∴AD′＝
＝AD＝
，∠
＝2∠BAC＝120°,
过点A作AH⊥EF于点H，
在Rt△
中，∠
＝30°,
∴
＝
·cos30°＝
,
∴△DEF周长的最小值为
；
（3）分类讨论：
①当内接等腰直角三角形的直角顶点在斜边AB上时，
如解图③，∵∠ACB＝∠EDF＝90°，
以EF为直径画圆，则点Ｃ、Ｄ在圆上，
连接CD，∵DE＝DF，
∴∠ACD＝∠BCD，又∵AC＝BC，
∴CD是AB边上的中线，点D是AB边的中点，
过点D作DE′⊥AC，DF′⊥BC，此时，DE′、DF′最短．
当点E与E′重合，点F与F′重合时，△DEF的面积最小，
此时四边形CEDF为矩形．
设DE＝x，则BC＝2DE＝2x＝6，
∴x＝3，∴S最小＝
；
②当内接等腰直角三角形的直角顶点在直角边上时，如解图④，
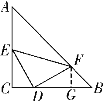
过点F作FG⊥BC于点G，设DG＝y，GF＝x，易证△CDE≌△GFD，
∴CD＝FG＝x，
∵∠B＝45°，FG⊥BC，
∴GB＝GF＝x，
∴BC＝CD＋DG＋GB＝2x＋y＝6，即y＝6－2x．
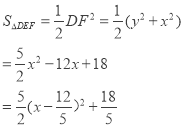
故当x=
时，
∵
,
∴△DEF的面积存在最小值，其最小值为
．
