Question

【题目】已知，在四边形中，为四边形的的平分线及外角的平分线所在的直线构成的锐角，若，，

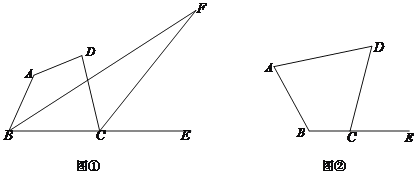
(1)如图①，当＞180°时，=_________(用含，的式子表示)；

(2)如图②，当＜180°时，请在图②中，画出，且______(用含，的式子表示)；

(3)当，满足条件_______时，不存在．

Answer 1

【答案】(1)90°；(2)画图见解析；90°－；(3)180°．

【解析】

（1）与（2）先根据四边形内角和等于360°，得出∠ABC+∠DCB=360°－（α+β），再根据邻补角的定义与三角形外角的性质定理和角平分线的定义整理即可得出结论；

（3）当∠F=0°时不存在，代入（1）或（2）题得出的结论即可得出α，β满足的关系式．

解：（1）∵∠ABC+∠DCB=360°－（α+β），

∴∠ABC+（180°－∠DCE）=360°－（α+β）=2∠FBC+（180°－2∠ECF）

=180°－2（∠ECF－∠FBC）=180°－2∠F，

∴360°－（α+β）=180°－2∠F，

∴；

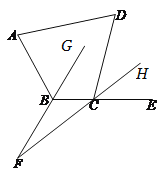
（2）画出的∠F如图所示，∵∠ABC+∠DCB=360°－（α+β），

∴∠ABC+（180°－∠DCE）=360°－（α+β）=2∠GBC+（180°－2∠HCE）

=180°+2（∠GBC－∠HCE）=180°+2（∠GBC－∠BCF）=180°+2∠F，

∴360°－（α+β）=180°+2∠F，

∴；

（3）由以上两题的结论知：当α+β=180°时，∠F=0°，故不存在∠F．

所以当α+β=180°时，不存在∠F．