题目内容
【题目】如图所示,等边![]() .
.
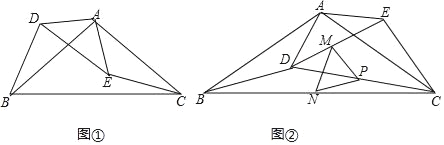
(1)如图(1),若![]() ,现有两点
,现有两点![]() 、
、![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,沿三角形的边顺时针运动,已知点
同时出发,沿三角形的边顺时针运动,已知点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .当点
.当点![]() 第一次到达
第一次到达![]() 点时,
点时,![]() 、
、![]() 同时停止运动.点
同时停止运动.点![]() ,
,![]() 运动______秒后,
运动______秒后,![]() 为等腰三角形.
为等腰三角形.

(2)如图,点![]() 位于等边
位于等边![]() 的内部,且
的内部,且![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①依题意,补全图形;
②若![]() ,
,![]() ,求
,求![]() 与
与![]() 的面积比.
的面积比.

【答案】(1)4秒,16秒;(2)①见解析;②1:4.
【解析】
(1)△AMN是以MN为底边等腰三角形时,证明△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB的长,列出方程,解方程得到答案;
(2)①利用射线的作法得出D点位置,并连接AD,CD;
②证明△CDP是等边三角形,求出AD,CD的长,作CM⊥BD于M,AN⊥BD于N,运用勾股定理求出CM,AN的长,再根据三角形面积公式求出面积比即可.
(1)设点M、N运动t秒后,可得到等边三角形△AMN,如图1,

AM=t,AN=AB-BN=12-2t,
∵△AMN是等边三角形,
∴AM=AN,即t=12-2t,
解得,t=4,
∴点M、N运动4秒后,可得到等边三角形AMN;
当点M、N在BC边上运动时,可以得到以MN为底的等腰三角形,如图2:

∵△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵AB=BC=AC,
∴△ACB是等边三角形,
∴∠C=∠B=60°,
在△ACM和△ABN中,
 ,
,
∴△ACM≌△ABN(AAS)
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y-12,NB=36-2y,
由题意得,y-12=36-2y,
解得:y=16.
若点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,M、N运动的时间为16秒.
(2)①如图所示,

②∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠PCA+∠PCB=60°,
∵∠PCA=∠CBP,
∴∠PCB+∠PBC=60°,
∴∠BPC=180°-60°=120°,
∵∠CPD=180°-∠BPC=60°,PD=PC,
∴△CDP是等边三角形,
∴CD=CP=PD=3,∠DCP=∠ACB=60°,
∴∠DCA=∠PCB,且CA=CB,
∴△DCA≌△PCB(SAS),
∴AD=PB,
∵![]()
∴AD=PB=12,
如图,作CM⊥BD于M,AN⊥BD于N.

∵∠CDP=∠ADP=60°,
∴DM=![]() PD=
PD=![]()
∴CM=![]() ,
,
由△DCA≌△PCB得∠ADC=∠BPC=120°,
∴∠ADP=60°,
∴DN=![]() ,
,
∴AN=![]()
∴

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案