题目内容
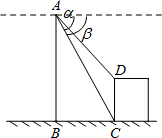
在坡角为30°的山坡上，一树的上部BC被台风“珍珠”括断后使树梢着地，且与山坡的坡面成30°角，若树梢着地处C与树根A的坡面距离为2米，求原来树的高度．（精确到0.01米）
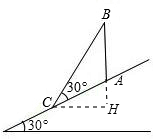
过点C作CH⊥BA，交BA的延长线于H．
则∠ACH=30°；（1分）
∵AC=2米，∴AH=1米；（2分）
CH=AC•cos30°=2×
=
（米）；（3分）
在Rt△BCH中，∠BCH=∠BCA+∠ACH=60°；
∴BC=2
米，BH=CH•tan60°=
•
=3（米）；（4分）
∴AB=BH-AH=3-1=2（米）；（5分）
∴AB+BC=2+2
≈5.46米．（6分）
答：原来树的高度为5.46米．
则∠ACH=30°；（1分）
∵AC=2米，∴AH=1米；（2分）
CH=AC•cos30°=2×
| ||
| 2 |
| 3 |
在Rt△BCH中，∠BCH=∠BCA+∠ACH=60°；
∴BC=2
| 3 |
| 3 |
| 3 |
∴AB=BH-AH=3-1=2（米）；（5分）
∴AB+BC=2+2
| 3 |
答：原来树的高度为5.46米．
练习册系列答案
小学课时特训系列答案
相关题目
