题目内容
右图中曲线是反比例函数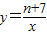 的图象的一支.
的图象的一支.(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?
(2)若一次函数
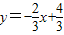 的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.
的图象与反比例函数的图象交于点A,与x轴交于点B,△AOB的面积为2,求n的值.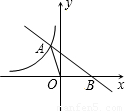
【答案】分析:(1)根据反比例函数的性质可求得反比例函数的图象分布在第二、第四象限,所以n+7<0即可求解;
(2)图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S= |k|,可利用△AOB的面积求出n值.
|k|,可利用△AOB的面积求出n值.
解答:解:(1)这个反比例函数图象的另一支位于第四象限.
由n+7<0,
解得n<-7,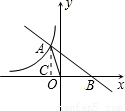
即常数n的取值范围是n<-7;
(2)在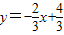 中令y=0,得x=2,
中令y=0,得x=2,
即OB=2.
过A作x轴的垂线,垂足为C,如图.
∵S△AOB=2,即 OB•AC=2,
OB•AC=2,
∴ ×2×AC=2,解得AC=2,即A点的纵坐标为2.
×2×AC=2,解得AC=2,即A点的纵坐标为2.
把y=2代入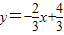 中,得x=-1,即A(-1,2).
中,得x=-1,即A(-1,2).
所以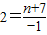 ,
,
解得n=-9.
点评:本题主要考查了反比例函数的性质和反比例函数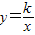 中k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|.
|k|.
(2)图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S=
 |k|,可利用△AOB的面积求出n值.
|k|,可利用△AOB的面积求出n值.解答:解:(1)这个反比例函数图象的另一支位于第四象限.
由n+7<0,
解得n<-7,

即常数n的取值范围是n<-7;
(2)在
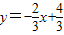 中令y=0,得x=2,
中令y=0,得x=2,即OB=2.
过A作x轴的垂线,垂足为C,如图.
∵S△AOB=2,即
 OB•AC=2,
OB•AC=2,∴
 ×2×AC=2,解得AC=2,即A点的纵坐标为2.
×2×AC=2,解得AC=2,即A点的纵坐标为2.把y=2代入
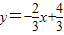 中,得x=-1,即A(-1,2).
中,得x=-1,即A(-1,2).所以
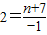 ,
,解得n=-9.
点评:本题主要考查了反比例函数的性质和反比例函数
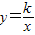 中k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
中k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S= |k|.
|k|. 
练习册系列答案
相关题目

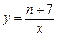 的图象的一支.
的图象的一支.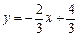 的图象与反比例函数的图象交于点A,与x轴交于点B,△
的图象与反比例函数的图象交于点A,与x轴交于点B,△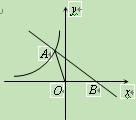
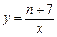 的图象的一支.
的图象的一支. 的图象与反比例函数的图象交于点A,与x轴交于点B,△
的图象与反比例函数的图象交于点A,与x轴交于点B,△
 的图象的一支.
的图象的一支. 的图象与反比例函数的图象交于点A,与x轴
的图象与反比例函数的图象交于点A,与x轴