Question

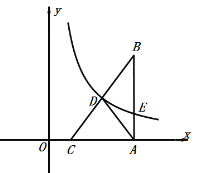
【题目】如图，在Rt△ABC中，，，，P为边BC上一动点， 于E，于F，M为EF的中点，则AM的最小值是（ ）

A.2.5B.2.4C.2D.3

Answer 1

【答案】B

【解析】

根据矩形的性质就可以得出EF，AP互相平分，且EF=AP，根据垂线段最短的性质就可以得出AP⊥BC时，AP的值最小，即AM的值最小，由勾股定理求出BC，根据面积关系建立等式求出其解即可．

∵PE⊥AB，PF⊥AC，∠BAC=90°，

∴∠EAF=∠AEP=∠AFP=90°，

∴四边形AEPF是矩形，

∴EF，AP互相平分．且EF=AP，

∴EF，AP的交点就是M点，

∵当AP的值最小时，AM的值就最小，

∴当AP⊥BC时，AP的值最小，即AM的值最小．

∵AP×BC=AB×AC，

∴AP×BC=AB×AC，

在Rt△ABC中，由勾股定理，得BC==10，

∵AB=6，AC=8，

∴10AP=6×8，

∴AP=，

∴AM=＝2.4，

故选B．