题目内容
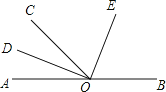
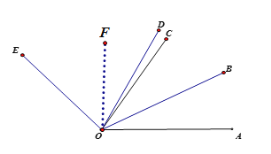
【题目】如图,已知∠AOB=30°,∠AOE=130°,OB平分∠AOC, OD平分∠AOE.
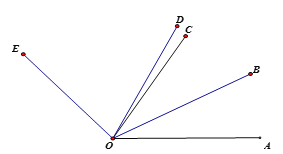
(1)求∠COD的度数;
(2)若以O为观测中心,OA为正东方向,则射线OD的方位角是 ;
(3)若∠AOC、射线OE分别以每秒5°、每秒3°的速度同时绕点O逆时针方向旋转,其他条件不变,当OA回到原处时,全部停止运动,则经过多长时间,∠BOE=28°?
【答案】(1)∠COD= 5°;(2)北偏东25°;(3)经过36秒或者64秒
【解析】
(1)由角平分线的定义求出∠AOD、∠AOC的度数,然后根据角的和差计算即可;
(2)作OF⊥OA,求出∠FOD的度数,然后根据方向角的表示方法,可得答案;
(3)设经过x秒,∠BOE=28°,分两种情况列出方程并解答即可.
(1)因为OB平分∠AOC, OD平分∠AOE,
所以∠AOC=2∠AOB=60°, ∠AOD=![]() ∠AOE=65°,
∠AOE=65°,
所以∠COD=∠AOD-∠AOC=65°-60°= 5° ;
(2)如图,作OF⊥OA,
∵∠AOD=65°,
∴∠FOD=90°-65°=25°,
∴射线OD的方位角是北偏东25°;
(3)因为∠AOB=30°,∠AOE=130°,
所以∠EOB=∠AOE-∠AOB=100°
设经过x秒∠BOE=28°,则3x+100-5x=28,
解得x=36 ;
或 5x-(3x+100)=28,
解得x=64.
答:经过36秒或者64秒∠BOE=28°.

练习册系列答案
相关题目