Question

【题目】如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，若PA=6，PB=8，PC=10，则∠APB=°．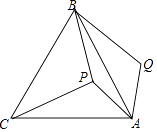

Answer 1

【答案】150
【解析】解：连结PQ，如图，

∵△ABC为等边三角形，

∴∠BAC=60°，AB=AC，

∵线段AP绕点A顺时针旋转60°得到线段AQ，

∴AP=PQ=6，∠PAQ=60°，

∴△APQ为等边三角形，

∴PQ=AP=6，

∵∠CAP+∠BAP=60°，∠BAP+∠BAQ=60°，

∴∠CAP=∠BAQ，

在△APC和△ABQ中，

，

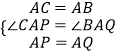∴△APC≌△ABQ，

∴PC=QB=10，

在△BPQ中，∵PB2=82=64，PQ2=62，BQ2=102，

而64+36=100，

∴PB2+PQ2=BQ2，

∴△PBQ为直角三角形，∠BPQ=90°，

∴∠APB=90°+60°=150°．

【考点精析】认真审题，首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)，还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形)的相关知识才是答题的关键．