题目内容
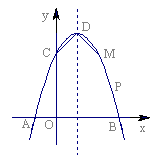
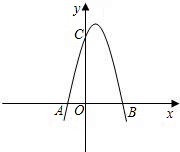
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3)。
⑴求抛物线的解析式;
⑵设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
⑶若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标。
证明:⑴∵抛物线与y轴交于点C(0,3),
∴设抛物线解析式为![]() ………………………………1分
………………………………1分
根据题意,得![]() ,解得
,解得![]()
∴抛物线的解析式为![]() ………………………………………2分
………………………………………2分
⑵存在。…………………………………………………………………………3分
由![]() 得,D点坐标为(1,4),对称轴为x=1。…………4分
得,D点坐标为(1,4),对称轴为x=1。…………4分
①若以CD为底边,则PD=PC,设P点坐标为(x,y),根据勾股定理,
得![]() ,即y=4-x。…………………………5分
,即y=4-x。…………………………5分
又P点(x,y)在抛物线上,∴![]() ,即
,即![]() …………6分
…………6分
解得![]() ,
,![]() ,应舍去。∴
,应舍去。∴![]() 。……………………7分
。……………………7分
∴![]() ,即点P坐标为
,即点P坐标为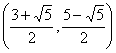 。……………………8分
。……………………8分
②若以CD为一腰,因为点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3)。
∴符合条件的点P坐标为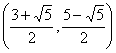 或(2,3)。……………………9分
或(2,3)。……………………9分
⑶由B(3,0),C(0,3),D(1,4),根据勾股定理,
得CB=![]() ,CD=
,CD=![]() ,BD=
,BD=![]() ,………………………………………………10分
,………………………………………………10分
∴![]() ,
,
∴∠BCD=90°,………………………………………………………………………11分
设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,在Rt△DCF中,
∵CF=DF=1,
∴∠CDF=45°,
由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3),
∴DM∥BC,
∴四边形BCDM为直角梯形, ………………………………………………………12分
由∠BCD=90°及题意可知,
以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;
以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在。
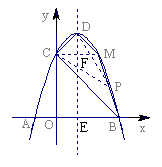 综上所述,符合条件的点M的坐标为(2,3)。…………………………………
综上所述,符合条件的点M的坐标为(2,3)。…………………………………

 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).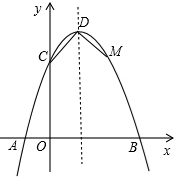 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1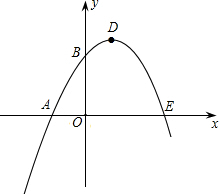 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )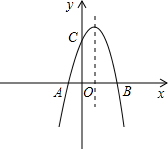 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).