题目内容
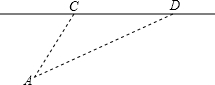如图，某校A与公路距离为3000米，又与该公路旁上的某车站D的距离为5000米，现要在公路边建一个商店C，使之与该校A及车站D的距离相等，则商店与车站的距离约为（ ）| A、875米 | B、3125米 | C、3500米 | D、3275米 |
分析：利用线段垂直平分线的性质可知C与该校A及车站D的距离相等，则点C在线段AD的垂直平分线上．依此解直角三角形即可．
解答：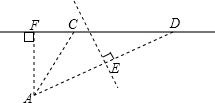
解：作AD的垂直平分线CE，作AF⊥CD，垂足为F．
则AF=3000，AD=5000．
根据勾股定理得 DF=4000．
∴cos∠D=
=
．
在直角△CED中，cos∠D=
=
=
，
∵AD=5000，
∴DE=2500．
∴
=
．
解得 CD=3125（米）．
故选B．
解：作AD的垂直平分线CE，作AF⊥CD，垂足为F．则AF=3000，AD=5000．
根据勾股定理得 DF=4000．
∴cos∠D=
| 4000 |
| 5000 |
| 4 |
| 5 |
在直角△CED中，cos∠D=
| 4000 |
| 5000 |
| 4 |
| 5 |
| DE |
| CD |
∵AD=5000，
∴DE=2500．
∴
| 4 |
| 5 |
| 2500 |
| CD |
解得 CD=3125（米）．
故选B．
点评：本题主要考查了垂直平分线的性质及解直角三角形的应用．
练习册系列答案
应用题作业本系列答案
相关题目
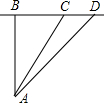如图，某校A与直线公路距离AB为3000米，又与该公路上某车站D的距离为5000米，现要在公路边建一个小商店C，使之与学校A及车站D的距离相等，那么，该店与车站D的距离是多少米？
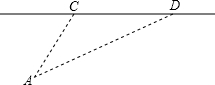如图，某校A与公路距离为3000米，又与该公路旁上的某车站D的距离为5000米，现要在公路边建一个商店C，使之与该校A及车站D的距离相等，则商店与车站的距离约为
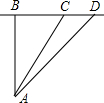如图，某校A与直线公路距离AB为3000米，又与该公路上某车站D的距离为5000米，现要在公路边建一个小商店C，使之与学校A及车站D的距离相等，那么，该店与车站D的距离是多少米？