题目内容
已知P在函数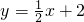 的图象上,A(-2,0),B(4,0),点P的横坐标为m,当△PAB为直角三角形时,求m的值.
的图象上,A(-2,0),B(4,0),点P的横坐标为m,当△PAB为直角三角形时,求m的值.
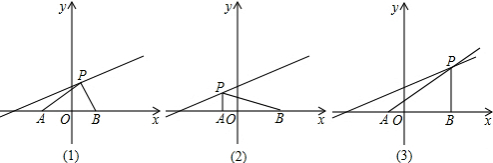
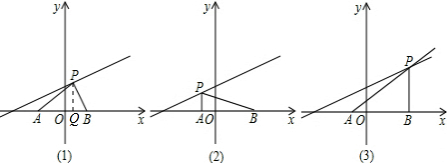
解:分三种情况考虑:
(1)当直角顶点为点P时,∠APB=90°,如图(1)所示,过P作PQ⊥AB,
∵点P在y=
 x+2上,∴设P(m,
x+2上,∴设P(m, m+2),
m+2),在Rt△APQ中,根据勾股定理得:AP2=(m+2)2+(
 m+2)2,
m+2)2,在Rt△BPQ中,根据勾股定理得:BP2=(4-m)2+(
 m+2)2,
m+2)2,在Rt△APB中,根据勾股定理得:AB2=AP2+BP2,即(m+2)2+(
 m+2)2+(4-m)2+(
m+2)2+(4-m)2+( m+2)2=36,
m+2)2=36,解得:m=±
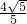 ;
;(2)当直角顶点为A(-2,0)时,∠PAB=90°,如图(2)所示,此时P的横坐标m=-2;
(3)当直角顶点为B(4,0)时,∠PBA=90°,如图(3)所示,此时P横坐标为m=4,
综上,当m=±
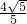 或m=-2或m=4时,△PAB为直角三角形.
或m=-2或m=4时,△PAB为直角三角形.分析:分三种情况考虑:(1)当直角顶点是P点时,如图(1)所示,由P在一次函数图象上,设P坐标为(m,
 m+2),过P作PQ垂直于AB,表示出AQ,在直角三角形APQ中,利用勾股定理表示出AP2,在直角三角形BPQ中,利用勾股定理表示出BP2,根据AB的长,利用勾股定理列出关于m的方程,求出方程的解得到m的值即可;(2)当A为直角顶点时,根据A坐标确定出m的值;(3)当B为直角顶点时,根据B坐标求出m的值即可.
m+2),过P作PQ垂直于AB,表示出AQ,在直角三角形APQ中,利用勾股定理表示出AP2,在直角三角形BPQ中,利用勾股定理表示出BP2,根据AB的长,利用勾股定理列出关于m的方程,求出方程的解得到m的值即可;(2)当A为直角顶点时,根据A坐标确定出m的值;(3)当B为直角顶点时,根据B坐标求出m的值即可.点评:此题属于一次函数综合题,涉及的知识有:坐标与图形性质,勾股定理,利用了分类讨论的思想,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
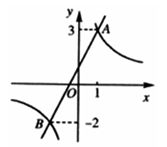
 的图象与反比例函数
的图象与反比例函数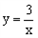 的图象相交于A、B两点。
的图象相交于A、B两点。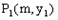 在一次函数的图象上,点
在一次函数的图象上,点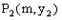 在反比函数的图象上。当
在反比函数的图象上。当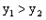 时,直接写出m的取值范围。
时,直接写出m的取值范围。