题目内容
【题目】如图, 在等边△ABC中, D, E, F分别为边AB, BC, CA上的点, 且满足∠DEF=60°.
(1)求证:![]() ;
;
(2)若DE⊥BC且DE=EF, 求![]() 的值.
的值.
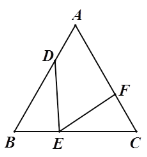
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由等边三角形的性质可知∠B=∠C=60°,再由已知条件和三角形外角的性质可证明∠BDE=∠FEC,进而证明△DBE∽△ECF,根据相似三角形的性质即可得出结论.
(2)由相似三角形的性质和已知条件得出BD=CE,由含30°角的直角三角形的性质得出BE![]() BD,即可得出结果.
BD,即可得出结果.
(1)∵△ABC是等边三角形,
∴∠B=∠C=60°,
又∵∠DEF=60°,
∴∠DEF=∠B.
∵∠DEC是△DBE的外角,
∴∠DEC=∠B+∠BDE,
即∠DEF+∠FEC=∠B+∠BDE.
∵∠DEF=∠B,
∴∠BDE=∠CEF,
又∵∠B=∠C,
∴△BDE∽△CEF,
∴![]() ,
,
∴BECE=BDCF;
(2)∵△BDE∽△CEF,
∴![]() ,
,
又∵DE=EF,即![]() ,
,
∴BD=CE.
∵DE⊥BC,
∴∠DEB=90°.
∵∠B=60°,
∴∠BDE=30°,
∴BE![]() BD,
BD,
∴![]() .
.

练习册系列答案
相关题目