��Ŀ����
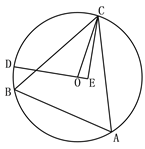
����Ŀ����ͼ1����һ�������۵��������ϣ���A��B�ֱ��ʾ��-9��4.
(1)A��B����֮��ľ���Ϊ________.
(2)��ͼ2������Ե�CΪ�۵㣬�������������Ҷ��ۣ���ʱ��A���ڵ�B���ұ�1����λ���ȴ������C��ʾ������________.
(3)��ͼ1������A��ÿ��3����λ���ȵ��ٶ������������˶�����B��ÿ��2����λ���ȵ��ٶ�Ҳ�����������˶�����ô��������ʱ�䣬A��B�������4����λ����?

���𰸡�(1)13��(2)-2��(3)t= 9���17��.
��������
��1����������������ľ��빫ʽ������⣻
��2�����C��ʾ������x���ֱ��ʾ��AC��BC���ٸ���AC-BC=1�г����̽�ɣ�
��3���˶�t���֪��A��ʾ����Ϊ-9+3t����B��ʾ����Ϊ4+2t���ٸ���AB�ľ���Ϊ4���ɵ÷��̣��ⷽ�̼��ɣ�
�⣺��1��AB=4-��-9��=13
��2�����C��ʾ������x��
��AC=x-��-9��=x+9��BC=4-x��
��A���ڵ�B���ұ�1����λ��
��AC-BC=1,
��AC-BC=x+9-��4-x��=2x+5=1��
��ã�x=-2��
���C��ʾ������-2��
�ʴ�Ϊ��-2��
(3) ���˶�t���A���B���4����λ��
�������֪��A��ʾ����Ϊ-9+3t����B��ʾ����Ϊ4+2t��
��![]() ��
��
��![]() ��
��![]()
���t=17��9.
���˶�9���17���A���B���4����λ��