题目内容
(2013•永安市质检)在一张长方形ABCD纸张中,AB=25cm,AD=20cm,现将这张纸片按下列图示方法折叠,请解决下列问题?(1)如图1,折痕为DE,点A的对应点F在CD上,则折痕DE的长为
(2)如图2,H、G分别为BC、AD的中点,点A的对应点F在HG上,折痕为DE,求重叠部分(△DEF)的面积;
(3)如图3,在图2中,把长方形ABCD沿着HG剪开,变成两张长方形纸片,将这两张纸按图形位置任意叠合后,发现重叠部分都是菱形,显然,这些菱形中周长最短是40cm.是否存在叠后周长最大的菱形?若存在,请求出叠合后周长最大的菱形的周长和面积;若不存在,请说明理由.

20
| 2 |
20
cm;| 2 |
(2)如图2,H、G分别为BC、AD的中点,点A的对应点F在HG上,折痕为DE,求重叠部分(△DEF)的面积;
(3)如图3,在图2中,把长方形ABCD沿着HG剪开,变成两张长方形纸片,将这两张纸按图形位置任意叠合后,发现重叠部分都是菱形,显然,这些菱形中周长最短是40cm.是否存在叠后周长最大的菱形?若存在,请求出叠合后周长最大的菱形的周长和面积;若不存在,请说明理由.

分析:(1)根据图形折叠的性质可知AD=AE=20cm,再根据勾股定理即可得出结论;
(2)由折叠的性质可得到DG=
AD=
DE,再根据直角三角形的性质得出∠EDA=30°,由锐角三角函数的定义得到AE的长,利用三角形的面积公式即可得出结论;
(3)设GK=x,则HK=25-x,利用勾股定理即可求出x的值,进而可得出菱形的周长求出其面积.
(2)由折叠的性质可得到DG=
| 1 |
| 2 |
| 1 |
| 2 |
(3)设GK=x,则HK=25-x,利用勾股定理即可求出x的值,进而可得出菱形的周长求出其面积.
解答: 解:(1)∵四边形ADFE是正方形,
解:(1)∵四边形ADFE是正方形,
∴DE=
=
=20
(cm);
故答案为:20
;
(2)由折叠的性质可知,AD=DF,
∵GH分别是AD、BC的中点,
∴GD=
AD=
DF
∴在Rt△DGE中,∠GFD=30°,∠GDF=60°,
∵∠GDE=∠EDF,
∴∠EDA=30°.
∴在Rt△ADE中,tan∠EDA=
,
∴AE=AD•tan30°=
∴S△DEF=
AE•AD=
×20×
=
;
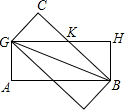 (3)最大的菱形如图所示:
(3)最大的菱形如图所示:
设GK=x,则HK=25-x,
x2=(25-x)2+102,
解得x=
,
则菱形的周长为58cm,
此时菱形的面积S=
×10=145.
 解:(1)∵四边形ADFE是正方形,
解:(1)∵四边形ADFE是正方形,∴DE=
| AD2+AE2 |
| 202+202 |
| 2 |
故答案为:20
| 2 |
(2)由折叠的性质可知,AD=DF,
∵GH分别是AD、BC的中点,
∴GD=
| 1 |
| 2 |
| 1 |
| 2 |
∴在Rt△DGE中,∠GFD=30°,∠GDF=60°,
∵∠GDE=∠EDF,
∴∠EDA=30°.
∴在Rt△ADE中,tan∠EDA=
| AE |
| AD |
∴AE=AD•tan30°=
20
| ||
| 3 |
∴S△DEF=
| 1 |
| 2 |
| 1 |
| 2 |
20
| ||
| 3 |
200
| ||
| 3 |
 (3)最大的菱形如图所示:
(3)最大的菱形如图所示:设GK=x,则HK=25-x,
x2=(25-x)2+102,
解得x=
| 29 |
| 2 |
则菱形的周长为58cm,
此时菱形的面积S=
| 29 |
| 2 |
点评:本题考查的是图形的翻折变换、菱形及矩形的性质、三角形的面积公式,熟知图形翻折变换的性质是解答此题的关键.

练习册系列答案
相关题目
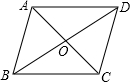 (2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是
(2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是 (2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数
(2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数