题目内容
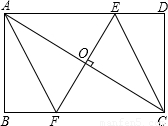
 已知:如图,EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由.
已知:如图,EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由.下面是某同学进行的推理,请你将他的推理过程补充完整.
证明:∵EG平分∠AEF,FH平分∠EFD(
已知
已知
),∴∠
GEF
GEF
=| 1 |
| 2 |
HFE
HFE
=| 1 |
| 2 |
∵∠AEF=∠EFD (已知)
∴∠
GEF
GEF
=∠HFE
HFE
(等量代换)∴EG∥FH(
内错角相等两直线平行
内错角相等两直线平行
).分析:首先根据角平分线的性质得到∠GEF=
∠AEF,∠HFE=
∠EFD,再根据∠AEF=∠EFD可得∠GEF=∠HFE,然后根据内错角相等,两直线平行可证出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明::∵EG平分∠AEF,FH平分∠EFD( 已知),
∴∠GEF=
∠AEF,∠HFE=
∠EFD(角平分线定义).
∵∠AEF=∠EFD (已知)
∴∠GEF=∠HFE(等量代换)
∴EG∥FH( 内错角相等两直线平行).
∴∠GEF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AEF=∠EFD (已知)
∴∠GEF=∠HFE(等量代换)
∴EG∥FH( 内错角相等两直线平行).
点评:此题主要考查了平行线的判定,关键是掌握平行线的判定定理;内错角相等,两直线平行.

练习册系列答案
相关题目
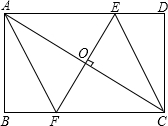 已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F.
已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F. 已知:如图,EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由.
已知:如图,EF分别交于AB、CD于E、F,∠AEF=∠EFD,EG平分∠AEF,FH平分∠EFD.试说明EG∥FH成立的理由. ∠AEF,∠________=
∠AEF,∠________=