题目内容
(2010•甘井子区模拟)已知:如图,EF是矩形ABCD的对角线AC的垂直平分线,EF与对角线AC及边AD、BC分别交于点O、E、F.(1)求证:四边形AFCE是菱形;
(2)如果FE=2ED,求AE:ED的值.

【答案】分析:(1)要证四边形AFCE是菱形,只需通过定义证明四边相等即可.此题实际是对判定菱形的方法“对角形垂直平分的四边形为菱形”的证明;
(2)根据平行四边形的对角线互相平分知,FE=2EO,又∵FE=2ED,可证Rt△OEC≌Rt△DEC,
又∠D=90°,∴EC=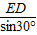 =2ED,∴AE=2ED,即AE:ED=2:1=2.
=2ED,∴AE=2ED,即AE:ED=2:1=2.
解答: (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠1=∠2.(1分)
∵EF垂直平分AC,
∴AO=CO,∠AOE=∠COF=90°,
∴△AOE≌△COF(ASA),
∴OE=OF(1分)
∴四边形AFEC是平行四边形.(1分)
又EF⊥AC,
∴四边形AFEC是菱形;(1分)
(2)解:由(1)知:FE=2EO,
又∵FE=2ED,
∴EO=ED,(1分)
又EO⊥AC,ED⊥DC,
∴∠3=∠4,(1分)
由(1)知,四边形AFEC是菱形,
∴AE=EC,∠2=∠3,
∴∠2=∠3=∠4= ∠BCD=30°(1分)
∠BCD=30°(1分)
又∠D=90°,
∴EC=2ED(1分)
∴AE=2ED,即AE:ED=2:1=2.(1分)
点评:本题利用了:1、中垂线的性质;2、矩形的性质;3、全等三角形的判定和性质;4、菱形的判定和性质;5、正弦的概念.
(2)根据平行四边形的对角线互相平分知,FE=2EO,又∵FE=2ED,可证Rt△OEC≌Rt△DEC,
又∠D=90°,∴EC=
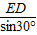 =2ED,∴AE=2ED,即AE:ED=2:1=2.
=2ED,∴AE=2ED,即AE:ED=2:1=2.解答:
 (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,∴AD∥BC,
∴∠1=∠2.(1分)
∵EF垂直平分AC,
∴AO=CO,∠AOE=∠COF=90°,
∴△AOE≌△COF(ASA),
∴OE=OF(1分)
∴四边形AFEC是平行四边形.(1分)
又EF⊥AC,
∴四边形AFEC是菱形;(1分)
(2)解:由(1)知:FE=2EO,
又∵FE=2ED,
∴EO=ED,(1分)
又EO⊥AC,ED⊥DC,
∴∠3=∠4,(1分)
由(1)知,四边形AFEC是菱形,
∴AE=EC,∠2=∠3,
∴∠2=∠3=∠4=
 ∠BCD=30°(1分)
∠BCD=30°(1分)又∠D=90°,
∴EC=2ED(1分)
∴AE=2ED,即AE:ED=2:1=2.(1分)
点评:本题利用了:1、中垂线的性质;2、矩形的性质;3、全等三角形的判定和性质;4、菱形的判定和性质;5、正弦的概念.

练习册系列答案
相关题目
(2010•甘井子区模拟)老师计算学生的学期总评成绩按照如下的标准:平时作业占10%,单元测验占30%,期中考试占25%,期末考试占35%,小贝和小嘉的成绩如下所示:
通过计算,你发现 的学期总评成绩高.
| 学生 | 平时作业 | 单元测验 | 期中考试 | 期末考试 |
| 小贝 | 80 | 75 | 71 | 88 |
| 小嘉 | 76 | 80 | 70 | 90 |





