题目内容
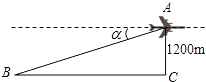 某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角α=16°31′,求飞机A到控制点B的距离.(精确到1米,sin16°31′=0.2843)
某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角α=16°31′,求飞机A到控制点B的距离.(精确到1米,sin16°31′=0.2843)
解:根据题意可得:AC=1200,∠ABC=α=16°31′;则AB=1200÷sin16°31′≈4221.
故飞机A到控制点B的距离约4221米.
分析:由题可知,在直角三角形中,知道已知角和对边,只需根据正弦值即可求出斜边.
点评:本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.另外还考查了利用计算器其三角函数值的知识.
故飞机A到控制点B的距离约4221米.
分析:由题可知,在直角三角形中,知道已知角和对边,只需根据正弦值即可求出斜边.
点评:本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.另外还考查了利用计算器其三角函数值的知识.

练习册系列答案
相关题目
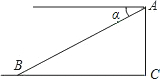 如图,某飞机于空中A处探测倒地面目标B,此时从飞机上看目标B的俯角α=30°,飞行高度AC=1200米,则飞机到目标B的距离AB为( )
如图,某飞机于空中A处探测倒地面目标B,此时从飞机上看目标B的俯角α=30°,飞行高度AC=1200米,则飞机到目标B的距离AB为( )| A、1200米 | ||
| B、2400米 | ||
C、400
| ||
D、1200
|
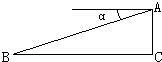 23、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看到地面控制点B的俯角α=17°,求飞机A到控制点B的距离.(精确到1米)
23、如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看到地面控制点B的俯角α=17°,求飞机A到控制点B的距离.(精确到1米)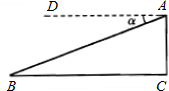 的俯角α=20°(B、C在同一水平线上),求目标C到控制点B的距离(精确到1米).
的俯角α=20°(B、C在同一水平线上),求目标C到控制点B的距离(精确到1米).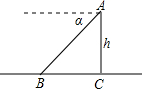 如图,某飞机于空中A处探测得地面目标C,此时飞行高度AC=h米,从飞机上看地面控制点B的俯角为α,那么飞机A到控制点B的距离是
如图,某飞机于空中A处探测得地面目标C,此时飞行高度AC=h米,从飞机上看地面控制点B的俯角为α,那么飞机A到控制点B的距离是 某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角α=16°31′,求飞机A到控制点B的距离.(精确到1米,sin16°31′=0.2843)
某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角α=16°31′,求飞机A到控制点B的距离.(精确到1米,sin16°31′=0.2843)