题目内容
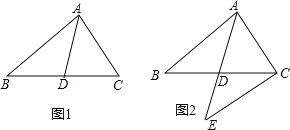
【题目】如图，在Rt△ABC中，∠ABC = 90°，BC = 1，AC =
．
（1）以点B为旋转中心，将△ABC沿逆时针方向旋转90°得到△A′BC′，请画出变换后的图形；
（2）求点A和点A′之间的距离．
【答案】（1）图形见解析（2）
【解析】
试题分析：（1）根据题意按要求逐步画图即可；
（2）连接AA’，然后根据旋转的性质和勾股定理可求解．
试题解析：（1）按要求画图，如图所示．
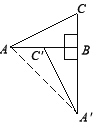
（2）连接A A′．
∵在Rt△ABC中，∠ABC=90°，BC=1，AC=
，
∴由勾股定理得AB=2．
∵以点B为旋转中心，将△ABC沿逆时针方向旋转90°得到△A′BC′，
∴A′B=AB=2．
∵在Rt△ABA′中，∠ABA′=90°，A′B=AB=2，
∴由勾股定理得AA′=
∴点A和点A′之间的距离是
练习册系列答案
相关题目
