题目内容
探索一元二次方程根与系数的关系:(1)填写下表:
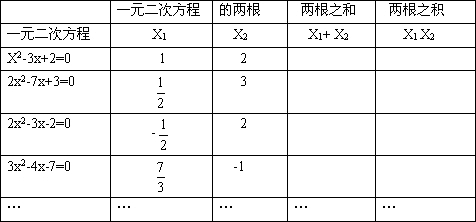
(2)若方程ax2+bx+c=0(a≠0,b2-4ac≥0),两根为x1、x2,根据上表的计算,你有何发现?写出你发现的规律;
(3)推导出你发现的规律.
分析:(1)根据题中所给的方程的根计算出两根之和与两根之积填表;
(2)根据表中两根之和、两根之积与方程系数的关系得出结论;
(3)根据求根公式证明一元二次方程根与系数的关系.
(2)根据表中两根之和、两根之积与方程系数的关系得出结论;
(3)根据求根公式证明一元二次方程根与系数的关系.
解答:解:(1)两根之和:3,
,
,
;两根之积:2,
,-1,-
;
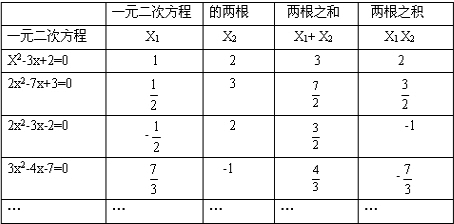
(2)由上表可知:x1+x2=-
;x1•x2=
.
证明:(3)∵ax2+bx+c=0(a≠0,b2-4ac≥0),
∴x1=
,
x2=
,(8分)
∴x1+x2=
+
=
,
=-
.(10分)
x1•x2=
•
=
=
.
=
.(12分)
| 7 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 7 |
| 3 |

(2)由上表可知:x1+x2=-
| b |
| a |
| c |
| a |
证明:(3)∵ax2+bx+c=0(a≠0,b2-4ac≥0),
∴x1=
-b+
| ||
| 2a |
x2=
-b-
| ||
| 2a |
∴x1+x2=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
=
| -2b |
| 2a |
=-
| b |
| a |
x1•x2=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
=
| b2-(b2-4ac) |
| 4a2 |
=
| 4ac |
| 4a2 |
=
| c |
| a |
点评:此题考查的是一元二次方程根与系数关系的推导过程,需同学们熟练掌握.

练习册系列答案
相关题目
(1)探索:解下列方程,将得到的两根x1,x2和x1+x2,x1•x2的值填入下面的表格.
(2)猜想:x1+x2,x1•x2的值与一元二次方程ax2+bx+c=0(a≠0)(x1,x2是其两个根)的各项系数a,b,c之间有何关系?
(3)利用一元二次方程的求根公式证明(2)中的猜想.
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | ||||
| 2x2+x-1=0 | ||||
| 3x2-5x+2=0 |
(3)利用一元二次方程的求根公式证明(2)中的猜想.
探索一元二次方程根与系数的关系:
(1)填写下表:

(2)若方程ax2+bx+c=0(a≠0,b2-4ac≥0),两根为x1、x2,根据上表的计算,你有何发现?写出你发现的规律;
(3)推导出你发现的规律.
(1)探索:解下列方程,将得到的两根x1,x2和x1+x2,x1•x2的值填入下面的表格.
(2)猜想:x1+x2,x1•x2的值与一元二次方程ax2+bx+c=0(a≠0)(x1,x2是其两个根)的各项系数a,b,c之间有何关系?
(3)利用一元二次方程的求根公式证明(2)中的猜想.
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | ||||
| 2x2+x-1=0 | ||||
| 3x2-5x+2=0 |
(3)利用一元二次方程的求根公式证明(2)中的猜想.
