题目内容
【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0.
【答案】
(1)解:∵二次函数y=﹣x2+2x+k+2与x轴有两个交点.
∴△=22﹣4×(﹣1)×(k+2)>0
解得:k>﹣3;
(2)解:当k=1时,二次函数是y=﹣x2+2x+3,
令y=0,得﹣x 2+2x+3=0,
解得:x 1=﹣1,x 2=3
∴抛物线与X轴的公共点A、B的坐标分别是(﹣1,0)、(3,0),
∵y=﹣x 2+2x+3=﹣(x﹣1)2+4
∴抛物线的顶点C的坐标是(1,4)
(3)解:由图象可知:当x=﹣1或x=3时,y=0;
当﹣1<x<3时,y>0.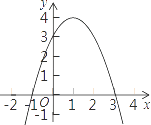
【解析】(1)抓住已知二次函数与x轴有两个交点得出b2-4ac>0,列不等式求出解集即可。
(2)将k=1代入函数解析式求出二次函数解析式,再根据y=0,解关于x的一元二次方程,求出x的值,就可得出抛物线与X轴的公共点A、B的坐标;然后将二次函数解析式配方成y=a(x-h)2+k的形式,就可求出其顶点坐标。
(3)先根据顶点坐标,抛物线与x轴的交点坐标、抛物线与y轴的交点坐标画出函数图像,再观察图像y>0,即是观察x轴上方的图像,就可写出自变量的取值范围。

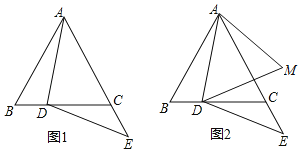
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
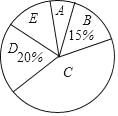
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 3 |
B | 4.25<x≤4.55 |
|
C | 4.55<x≤4.85 | 18 |
D | 4.85<x≤5.15 | 8 |
E | 5.15<x≤5.45 |
|
根据以上信息,解谷下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人;
(2)本次调查的样本容量是 ,视力在5.15<x≤5.45范围内学生数占被调查学生数的百分比是 %;
(3)在统计图中,C组对应扇形的圆心角度数为 °;
(4)若该校九年级有400名学生,估计视力超过4.85的学生数.