题目内容
【题目】如图,点A(1,0),B(0, ![]() )分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
)分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求直线AB的解析式及点C的坐标;
(2)若点P(m, ![]() )为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.
)为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.

【答案】(1)y=![]() x+
x+![]() ,点C(2,
,点C(2, ![]() );(2)m=
);(2)m=![]() 或
或![]() .
.
【解析】试题分析:
(1) 根据一次函数的一般形式,利用点A和点B的坐标,可以获得关于一般形式中待定系数的方程,求解这些方程即可确定直线AB的解析式. 要求点C的坐标,可以过点C作x轴的垂线CD,只要求得线段OD和CD的长即可. 由于已知线段OA的长,所以实际上只需要获得线段AD和CD的长. 利用已知条件可以求得线段AB的长和∠OAB的值,进而可以得到线段AC的长和∠CAD的值,利用Rt△CAD中的几何关系即可求得线段AD和CD的长.
(2) 根据点P坐标的特征和线段OB的长,可以确定点P在OB的垂直平分线上. 根据第(1)小题求得的线段长度易知△ABC的面积,也就得到了△APB的面积. 利用OB的垂直平分线将△APB的面积分割为两部分进行计算,不难获得△APB的面积与点P和线段AB的中点F的距离PF的关系式,进而可以求得线段PF的长. 通过两点之间距离的表达式可以求得点P的坐标,从而获得m的值.
试题解析:
(1) 
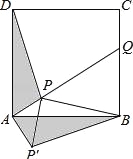
如图,过点C作CD⊥OA,垂足为D.
设直线AB的解析式为y=kx+b (k≠0).
将点A的坐标(1, 0)与点B的坐标(0, ![]() )代入该直线的解析式,得
)代入该直线的解析式,得
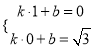 ,
,
解之,得
 .
.
∴直线AB的解析式为![]() .
.
∵点A的坐标是(1, 0),点B的坐标是(0, ![]() ),
),
∴OA=1,OB=![]() ,
,
∴在Rt△AOB中, ![]() .
.
∵在Rt△ABC,∠ABC=30°,
∴![]() ,
,
∵在Rt△ABC中,AB2=BC2-AC2=(2AC)2-AC2=3AC2=22=4,
∴AC=![]() .
.
∵在Rt△AOB中, ![]() ,
,
∴∠OBA=30°,
∴在Rt△AOB中,∠OAB=90°-∠OBA=60°,
∵∠BAC=90°,
∴∠CAD=180°-∠BAC-∠OAB=180°-90°-60°=30°.
∴在Rt△CAD中, ![]() ,
,
 ,
,
∴OD=OA+AD=1+1=2.
∴点C的坐标为(2, ![]() ).
).
(2) 
如图,作线段OB的垂直平分线MN,交OB于点G,交AB于点F. 过点A作AE⊥MN,垂足为E.
∵OB=![]() ,点P的纵坐标为
,点P的纵坐标为![]() ,
,
∴点P在OB的垂直平分线MN上.
∵Rt△ABC的面积为![]() ,
,
∴△APB的面积为![]() ,即△AFP的面积与△BFP的面积之和为
,即△AFP的面积与△BFP的面积之和为![]() ,
,
∴![]() .
.
∵AE+BG=OB=![]() ,
,
∴![]() ,
,
∴![]() .
.
∵点F在OB的垂直平分线MN上,
∴![]() ,
,
∴点F的坐标为(![]() ,
, ![]() ).
).
∵点F的坐标为(![]() ,
, ![]() ),点P的坐标为(m,
),点P的坐标为(m, ![]() ),
),
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
即m的值为![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某服装点用6000购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?