题目内容
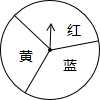小明和小亮用如下的同一个转盘进行“配紫色”游戏．游戏规则如下：连续转动两次转盘，如果两次转盘转出的颜色相同或配成紫色（若其中一次转盘转出蓝色，另一次转出红色，则可配成紫色），则小明得1分，否则小亮得1分．你认为这个游戏对双方公平吗？请说明理由；若不公平，请你修改规则使游戏对双方公平．
分析：游戏是否公平，关键要看是否游戏双方赢的机会是否相等，即判断双方取胜的概率是否相等，或转化为在总情况明确的情况下，判断双方取胜所包含的情况数目是否相等．
解答：解：
（2分）
从表中可以得到：P（小明获胜）=
，P（小亮获胜）=
．
∴小明的得分为
×1=
，小亮的得分为
×1=
．
∵
＞
，
∴游戏不公平．（4分）
修改规则不唯一．如若两次转出颜色相同或配成紫色，则小明得4分，否则小亮得5分．（6分）
| 第二次 第一次 |
红 | 黄 | 蓝 |
| 红 | （红，红） | （红，黄） | （红，蓝） |
| 黄 | （黄，红） | （黄，黄） | （黄，蓝） |
| 蓝 | （蓝，红） | （蓝，黄） | （蓝，蓝） |
从表中可以得到：P（小明获胜）=
| 5 |
| 9 |
| 4 |
| 9 |
∴小明的得分为
| 5 |
| 9 |
| 5 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
∵
| 5 |
| 9 |
| 4 |
| 9 |
∴游戏不公平．（4分）
修改规则不唯一．如若两次转出颜色相同或配成紫色，则小明得4分，否则小亮得5分．（6分）
点评：本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
一课一练课时达标系列答案
相关题目
小明和小亮两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，
实验的结果如下：
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
（1）请计算“3点朝上”的频率和“5点朝上”的频率．
（2）一位同学说：“根据实验，一次实验中出现5点朝上的概率最大”。这位同学的说法正确吗？为什么？
（3）小明和小亮各投掷一枚骰子，用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
小明和小亮两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们实验的结果如下：
（1）请计算“3点朝上”的频率和“5点朝上”的频率．
（2）一位同学说：“根据实验，一次实验中出现5点朝上的概率最大”．这位同学的说法正确吗？为什么？
（3）小明和小亮各投掷一枚骰子，用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
（2）一位同学说：“根据实验，一次实验中出现5点朝上的概率最大”．这位同学的说法正确吗？为什么？
（3）小明和小亮各投掷一枚骰子，用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
小明和小亮两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们实验的结果如下：
（1）请计算“3点朝上”的频率和“5点朝上”的频率．
（2）一位同学说：“根据实验，一次实验中出现5点朝上的概率最大”．这位同学的说法正确吗？为什么？
（3）小明和小亮各投掷一枚骰子，用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
（2）一位同学说：“根据实验，一次实验中出现5点朝上的概率最大”．这位同学的说法正确吗？为什么？
（3）小明和小亮各投掷一枚骰子，用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．