题目内容
【题目】有这样一对数:一个数的数字排列完全颠倒过来就变成另一个数,简单地说就是顺序相反的两个数,我们把这样的一对数互称为反序数.比如:68的反序数是86,235的反序数是532,4056的反序数是6504.根据以上阅读材料,回答下列问题:
(1)已知一个三位数,其数位上的数字为连续的三个自然数,请写出满足条件的一对反序数 与 ,并求出原三位数与其反序数之差的绝对值 ;
(2)如果一个两位数等于其反序数与1的平均数,求这个两位数;
(3)若一个两位数在其中间插入一个数字![]() (
(![]() ,
,![]() 为整数),得到的这个三位数是原来两位数的9倍,请求出满足条件的两位数的反序数.
为整数),得到的这个三位数是原来两位数的9倍,请求出满足条件的两位数的反序数.
【答案】(1)123与321(答案不唯一);198(2)37;(3)51、52、53、54
【解析】试题分析:(1)根据反序数的定义即可写出反序数;
(2)设这个两位数为10a+b,则其反序数为10b+a,根据一个两位数等于其反序数与1的平均数列出方程求解即可;
(3)先根据题意求出原来两位数,再求出满足条件的两位数的反序数.
试题解析:(1)123与321(答案不唯一);198
(2)设这个两位数为10a+b ,则反序数为10b+a
∴10a+b=![]() (10b+a+1)
(10b+a+1)
b=![]()
∵a、b均为正整数,且1≤a≤9,1≤b≤9
∴a=3,b=7
∴这个两位数是37;
(3)设这个两位数为10x+y,(x、y为整数,且1≤x≤9,1≤y≤9)
100x+10k+y=9(10x+y)
10(x+k)=8y,即8y是10的倍数
∵k、x、y为整数,且![]() ,1≤x≤9,1≤y≤9
,1≤x≤9,1≤y≤9
∴x+k≠0,y=5,
∴x+k =4
∴x=1或x=2或x=3或![]()
∴这个两位数的反序数为:51、52、53、54

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 |
| 78 | 88 |
相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 |
|
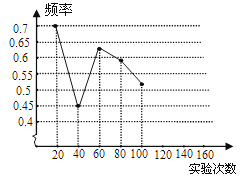
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少?
