题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F. 
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
【答案】
(1)解:如图,连接OD、CD,
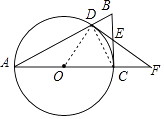
∵AC为⊙O的直径,
∴△BCD是直角三角形,
∵E为BC的中点,
∴BE=CE=DE,
∴∠CDE=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠DCE=90°,
∴∠ODC+∠CDE=90°,即OD⊥DE,
∴DE是⊙O的切线
(2)解:设⊙O的半径为r,
∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2,
解得:r=3,
∴⊙O的直径为6
【解析】(1)连接OD、CD,由AC为⊙O的直径知△BCD是直角三角形,结合E为BC的中点知∠CDE=∠DCE,由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案;(2)设⊙O的半径为r,由OD2+DF2=OF2 , 即r2+42=(r+2)2可得r=3,即可得出答案.

练习册系列答案
相关题目
【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?