题目内容
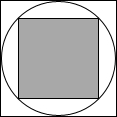 (2013•烟台模拟)如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为
(2013•烟台模拟)如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为| 1 |
| 2 |
| 1 |
| 2 |
分析:根据几何概率的意义,求出小圆面积与大圆面积的比即为小球落在小圆内部区域(阴影部分)的概率.
解答: 解:设小正方形的边长为1,则其面积为1.
解:设小正方形的边长为1,则其面积为1.
∵圆的直径正好是大正方形边长,
∴根据勾股定理,其小正方形对角线为
,即圆的直径为
,
∴大正方形的边长为
,
则大正方形的面积为
×
=2,则小球停在小正方形内部(阴影)区域的概率为
.
故答案为:
.
 解:设小正方形的边长为1,则其面积为1.
解:设小正方形的边长为1,则其面积为1.∵圆的直径正好是大正方形边长,
∴根据勾股定理,其小正方形对角线为
| 2 |
| 2 |
∴大正方形的边长为
| 2 |
则大正方形的面积为
| 2 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题考查了几何概率,解答此题除了熟悉几何概率的定义外,还要熟悉圆内接正方形和圆内切正方形的性质.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目

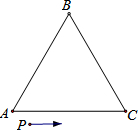 (2013•烟台模拟)如图一小虫从P点出发绕边长为10cm的等边三角形ABC爬行一圈回到点P,在小虫爬行过程中,始终保持与三角形ABC的边的距离是2cm,求小虫爬过的路径的长是
(2013•烟台模拟)如图一小虫从P点出发绕边长为10cm的等边三角形ABC爬行一圈回到点P,在小虫爬行过程中,始终保持与三角形ABC的边的距离是2cm,求小虫爬过的路径的长是