题目内容
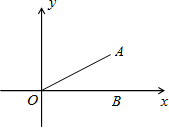 如图,已知OA=6,∠AOB=30°,则经过点A的反比例函数的解析式为( )
如图,已知OA=6,∠AOB=30°,则经过点A的反比例函数的解析式为( )A、y=-
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
分析:首先根据直角三角形的性质求出AC=3,再根据勾股定理求出OC的长,从而得到A点坐标,再利用待定系数法求出反比例函数解析式.
解答: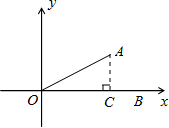 解:如图,过A点作AC⊥x轴于点C,
解:如图,过A点作AC⊥x轴于点C,
∵∠AOB=30°,
∴AC=
OA,
∵OA=6,
∴AC=3,
在Rt△ACO中,
OC2=AO2-AC2,
∴OC=
=3
,
∴A点坐标是:(3
,3),
设反比例函数解析式为y=
,
∵反比例函数的图象经过点A,
∴k=3×3
=9
,
∴反比例函数解析式为y=
.
故选B.
 解:如图,过A点作AC⊥x轴于点C,
解:如图,过A点作AC⊥x轴于点C,∵∠AOB=30°,
∴AC=
| 1 |
| 2 |
∵OA=6,
∴AC=3,
在Rt△ACO中,
OC2=AO2-AC2,
∴OC=
| 62-32 |
| 3 |
∴A点坐标是:(3
| 3 |
设反比例函数解析式为y=
| k |
| x |
∵反比例函数的图象经过点A,
∴k=3×3
| 3 |
| 3 |
∴反比例函数解析式为y=
9
| ||
| x |
故选B.
点评:此题主要考查了直角三角形的性质,勾股定理,以及待定系数法求反比例函数解析式,做题的关键是根据勾股定理求出A点的坐标.

练习册系列答案
相关题目
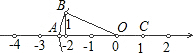 如图,已知OA=OB,那么数轴上点A与点C的距离是
如图,已知OA=OB,那么数轴上点A与点C的距离是
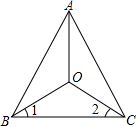 如图,已知OA平分∠BAC,∠1=∠2,求证:△AOB≌△AOC.
如图,已知OA平分∠BAC,∠1=∠2,求证:△AOB≌△AOC.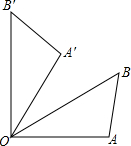 如图,已知△OA′B′是△OAB绕点O逆时针旋转60°得到的,那么△OA′B′与△OAB的关系是
如图,已知△OA′B′是△OAB绕点O逆时针旋转60°得到的,那么△OA′B′与△OAB的关系是