题目内容
金银花自古被誉为清热解毒的良药,同时也是很多高级饮料的常用原料.“渝蕾一号”为重庆市中药研究院所选育的金银花优良品种,较传统金银花具有质量好、产量高、结蕾整齐等优点.某花农于前年引进一批“渝蕾一号”金银花种苗进行种植,去年第一次收获.因金银花入药或作饮料需要使用干燥花蕾,该花农将收获的新鲜金银花全部干燥成干花蕾后出售.根据经验,每亩鲜花蕾产量 (千克)与每亩种苗数
(千克)与每亩种苗数 (株)满足关系式:
(株)满足关系式: ,每亩成本
,每亩成本 (元)与每亩种苗数
(元)与每亩种苗数 (株)之间的函数关系满足下表:
(株)之间的函数关系满足下表:
|
每亩种苗数 |
100 |
110 |
120 |
130 |
140 |
|
每亩成本 |
1800 |
1860 |
1920 |
1980 |
2040 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求出 与
与 的函数关系式;
的函数关系式;
(2)若该品种金银花的折干率为20%(即每100千克鲜花蕾,干燥后可得20千克干花蕾),去年每千克干花蕾售价为200元,则当每亩种苗数 为多少时,每亩销售利润
为多少时,每亩销售利润 可获得最大值,并求出该最大利润;(利润=收入
可获得最大值,并求出该最大利润;(利润=收入 成本)
成本)
(3)若该花农按照(2)中获得最大利润的方案种植,并不断改善种植技术,今年每亩鲜花蕾产量比去年增加 %.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低
%.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低 %,结果今年每亩销售总额为45810元.请你参考以下数据,估算出
%,结果今年每亩销售总额为45810元.请你参考以下数据,估算出 的整数值(
的整数值( ).
).
(参考数据: ,
, ,
, ,
, )
)
(1)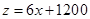 (2)当每亩种苗数为
(2)当每亩种苗数为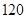 株时,每亩销售利润
株时,每亩销售利润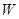 可获得最大值,最大利润为
可获得最大值,最大利润为 元(3)9
元(3)9
【解析】(1)用待定系数法求得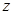 与
与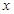 的函数关系式
的函数关系式
(2)由题意列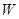 于
于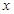 的关系式,进行讨论
的关系式,进行讨论
(3)根据题意设 ,代入原方程求解
,代入原方程求解
解:(1)由表格知,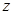 为
为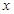 的一次函数,设
的一次函数,设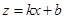 (
(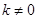 )
)
∵当 时,
时,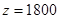 ;当
;当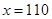 时,
时,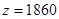
∴ 解得
解得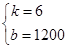
∴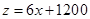
当 时,
时,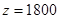
经检验,表格中每组数据均满足该关系式
∴该函数关系式为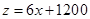
(2)由题意知,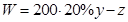
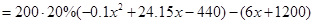
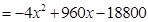

∵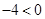
∴当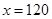 时,
时,
∴当每亩种苗数为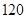 株时,每亩销售利润
株时,每亩销售利润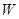 可获得最大值,最大利润为
可获得最大值,最大利润为 元.
元.
(3)当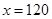 时,
时,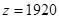
∴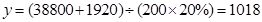
根据题意有
设 ,则原方程可化为
,则原方程可化为
解得 
∴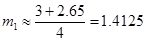 ,
,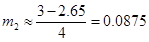
∴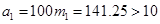 (舍去)
(舍去) 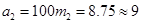
∴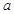 的值约为
的值约为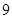 .
.

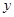 (千克)与每亩种苗数
(千克)与每亩种苗数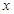 (株)满足关系式:
(株)满足关系式: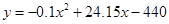 ,每亩成本
,每亩成本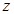 (元)与每亩种苗数
(元)与每亩种苗数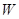 可获得最大值,并求出该最大利润;(利润=收入
可获得最大值,并求出该最大利润;(利润=收入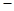 成本)
成本)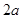 %.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低
%.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低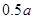 %,结果今年每亩销售总额为45810元.请你参考以下数据,估算出
%,结果今年每亩销售总额为45810元.请你参考以下数据,估算出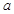 的整数值(
的整数值(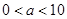 ).
).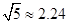 ,
,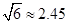 ,
,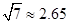 ,
,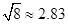 )
)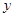 (千克)与每亩种苗数
(千克)与每亩种苗数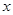 (株)满足关系式:
(株)满足关系式: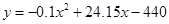 ,每亩成本
,每亩成本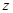 (元)与每亩种苗数
(元)与每亩种苗数
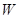 可获得最大值,并求出该最大利润;(利润=收入
可获得最大值,并求出该最大利润;(利润=收入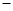 成本)
成本)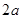 %.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低
%.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低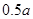 %,结果今年每亩销售总额为45810元.请你参考以下数据,估算出
%,结果今年每亩销售总额为45810元.请你参考以下数据,估算出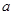 的整数值(
的整数值(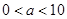 ).
).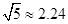 ,
,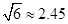 ,
,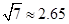 ,
,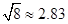 )
)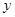 (千克)与每亩种苗数
(千克)与每亩种苗数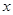 (株)满足关系式:
(株)满足关系式: ,每亩成本
,每亩成本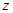 (元)与每亩种苗数
(元)与每亩种苗数
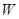 可获得最大值,并求出该最大利润;(利润=收入
可获得最大值,并求出该最大利润;(利润=收入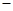 成本)
成本)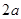 %.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低
%.但由于市场上同类产品数量猛增,造成每千克干花蕾的售价比去年降低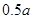 %,结果今年每亩销售总额为45810元.请你参考以下数据,估算出
%,结果今年每亩销售总额为45810元.请你参考以下数据,估算出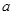 的整数值(
的整数值(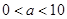 ).
).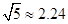 ,
,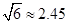 ,
,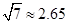 ,
,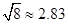 )
)