��Ŀ����
��2012•�ij�һģ����һƽֱ�Ӱ�lͬ����A��B������ׯ��A��B��l�ľ���ֱ���3km��2km��AB=akm��a��1�����ּƻ��ںӰ�l�Ͻ�һ��ˮվP������ˮ����������ׯ��ˮ��
ij����ѧ��ȤС���������������ܵ�������ͼ1�Ƿ���һ��ʾ��ͼ����÷����йܵ�����Ϊd1����d1=PB+BA��km��������BP��l�ڵ�P����ͼ2�Ƿ�������ʾ��ͼ����÷����йܵ�����Ϊd2����d2=PA+PB��km�������е�A�����A����l�Գƣ�A��B��l���ڵ�P����
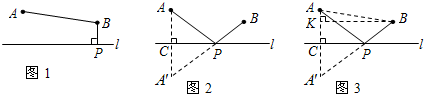
�۲���㣺��1���ڷ���һ�У�d1=
��2���ڷ������У��鳤С��Ϊ�˼���d2�ij���������ͼ3��ʾ�ĸ����ߣ����㰴С��ͬѧ��˼·���㣬d2=
km���ú�a��ʽ�ӱ�ʾ����
̽�����ɣ���1���ٵ�a=4ʱ���Ƚϴ�С��d1
�ڵ�a=6ʱ���Ƚϴ�С��d1
��2������ο�����ָ������a����a��1ʱ��������ȡֵ������з�����Ҫʹ����Ĺܵ����Ƚ϶̣�Ӧѡ��һ���Ƿ�������
����ָ����������ֱ�ӱȽ���������m��n�Ĵ�Сʱ�����Զ����ǵ�ƽ�����бȽϣ�
��m2-n2=��m+n����m-n����m+n��0��
�ࣨm2-n2���루m-n���ķ�����ͬ��
��m2-n2��0ʱ��m-n��0����m��n��
��m2-n2=0ʱ��m-n=0����m=n��
��m2-n2��0ʱ��m-n��0����m��n��
ij����ѧ��ȤС���������������ܵ�������ͼ1�Ƿ���һ��ʾ��ͼ����÷����йܵ�����Ϊd1����d1=PB+BA��km��������BP��l�ڵ�P����ͼ2�Ƿ�������ʾ��ͼ����÷����йܵ�����Ϊd2����d2=PA+PB��km�������е�A�����A����l�Գƣ�A��B��l���ڵ�P����

�۲���㣺��1���ڷ���һ�У�d1=
a+2
a+2
km���ú�a��ʽ�ӱ�ʾ������2���ڷ������У��鳤С��Ϊ�˼���d2�ij���������ͼ3��ʾ�ĸ����ߣ����㰴С��ͬѧ��˼·���㣬d2=
| a2+24 |
| a2+24 |
̽�����ɣ���1���ٵ�a=4ʱ���Ƚϴ�С��d1
��
��
d2�����������=�����������ڵ�a=6ʱ���Ƚϴ�С��d1
��
��
d2�����������=������������2������ο�����ָ������a����a��1ʱ��������ȡֵ������з�����Ҫʹ����Ĺܵ����Ƚ϶̣�Ӧѡ��һ���Ƿ�������
����ָ����������ֱ�ӱȽ���������m��n�Ĵ�Сʱ�����Զ����ǵ�ƽ�����бȽϣ�
��m2-n2=��m+n����m-n����m+n��0��
�ࣨm2-n2���루m-n���ķ�����ͬ��
��m2-n2��0ʱ��m-n��0����m��n��
��m2-n2=0ʱ��m-n=0����m=n��
��m2-n2��0ʱ��m-n��0����m��n��
�������۲���㣺��1����������Ե�֪�ܵ�����Ϊd1=PB+BA��km��������BP��l�ڵ�P�ó�PB=2���ʿ��Եó�d1��ֵΪa+2��
��2�����������ݹ��ɶ����������KB��ֵ������Գƿ��������K��ֵ����Rt��KBA���ɹ��ɶ����������A��B��ֵ
���ǹܵ����ȣ�
̽�����ɣ���1���ٰ�a=4����d1=a+2��d2=
�Ϳ��ԱȽ����С��
�ڰ�a=6����d1=a+2��d2=
�Ϳ��ԱȽ����С��
��2������������۵�d1��d2��d1=d2��d1��d2ʱ�Ϳ��Էֱ����a�ķ�Χ���Ӷ�ȷ��ѡ����
��2�����������ݹ��ɶ����������KB��ֵ������Գƿ��������K��ֵ����Rt��KBA���ɹ��ɶ����������A��B��ֵ
| a2+24 |
̽�����ɣ���1���ٰ�a=4����d1=a+2��d2=
| a2+24 |
�ڰ�a=6����d1=a+2��d2=
| a2+24 |
��2������������۵�d1��d2��d1=d2��d1��d2ʱ�Ϳ��Էֱ����a�ķ�Χ���Ӷ�ȷ��ѡ����
����⣺��1����BP��l��
��BP=2��
��AB=a��
��d1=a+2��
��2���ߵ�A�����A����l�Գƣ�
��AA��=6��
��BK��AA�䣬
��AK=1����Rt��ABK�У��ɹ��ɶ�������
��BK2=a2-1��
��Rt��KBA���ɹ��ɶ�������
A��B2=25+a2-1=a2+24��
��A��B=
̽������
��1���ٵ�a=4ʱ��d1=6��d2=2
��
��6��2
��
��d1��d2��
�ڵ�a=6ʱ��d1=8��d2=2
��
��8��2
��
��d1��d2��
��2����d12-d22=��a+2��2-��
��2=4a-20��
��ٵ�4a-20��0����a��5ʱ��d1��d2��
��ѡ��������ܵ��϶̣�
�ڵ�4a-20=0��a=5ʱ��d1=d2��
��ѡ��һ��������ܵ�һ����
�۵�4a-20��0����a��5ʱ��d1��d2��
��ѡ��һ����ܵ��϶̣�
���Ͽ�֪����a��5ʱ��ѡ��������
��a=5ʱ��ѡ����һ������
��1��a��5 ʱ��ѡ����һ��
�ʴ�Ϊ��a+2��
����������
��BP=2��
��AB=a��
��d1=a+2��
��2���ߵ�A�����A����l�Գƣ�
��AA��=6��
��BK��AA�䣬
��AK=1����Rt��ABK�У��ɹ��ɶ�������
��BK2=a2-1��
��Rt��KBA���ɹ��ɶ�������
A��B2=25+a2-1=a2+24��
��A��B=
| a2+24 |
̽������
��1���ٵ�a=4ʱ��d1=6��d2=2
| 10 |
��6��2
| 10 |
��d1��d2��
�ڵ�a=6ʱ��d1=8��d2=2
| 15 |
��8��2
| 15 |
��d1��d2��
��2����d12-d22=��a+2��2-��
| a2+24 |
��ٵ�4a-20��0����a��5ʱ��d1��d2��
��ѡ��������ܵ��϶̣�
�ڵ�4a-20=0��a=5ʱ��d1=d2��
��ѡ��һ��������ܵ�һ����
�۵�4a-20��0����a��5ʱ��d1��d2��
��ѡ��һ����ܵ��϶̣�
���Ͽ�֪����a��5ʱ��ѡ��������
��a=5ʱ��ѡ����һ������
��1��a��5 ʱ��ѡ����һ��
�ʴ�Ϊ��a+2��
| a2+24 |
���������⿼������ԳƵ����ʵ����ã����·��������ѧģʽ�����ã����ɶ��������ã����Ĵ�С�ıȽϷ��������ã�

��ϰ��ϵ�д�
�����Ŀ
 ��ƽ������ ��
��ƽ������ ��