题目内容
【题目】如图,△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC.则BN:NQ:QM等于( )

A. 6:3:2 B. 2:1:1 C. 5:3:2 D. 1:1:1
【答案】C
【解析】
连结MF,如图,先证明MF为△CEA的中位线,则AE=2MF,AE∥MF,利用NE∥MF得到 ![]() ,
,![]() ,即BN=NM,MF=2NF,设BN=a,NE=b,则NM=a,MF=2b,AE=4b,所以AN=3b,然后利用AN∥MF得到
,即BN=NM,MF=2NF,设BN=a,NE=b,则NM=a,MF=2b,AE=4b,所以AN=3b,然后利用AN∥MF得到 ![]() ,所以NQ=
,所以NQ=![]() a,QM=
a,QM=![]() a,再计算BN:NQ:QM的值.
a,再计算BN:NQ:QM的值.
连结MF,如图,
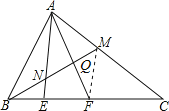
∵M是AC的中点,EF=FC,
∴MF为△CEA的中位线,
∴AE=2MF,AE∥MF,
∵NE∥MF,
∴![]() ,
,![]() ,
,
∴BN=NM,MF=2NF,
设BN=a,NE=b,则NM=a,MF=2b,AE=4b,
∴AN=3b,
∵AN∥MF,
∴![]() ,
,
∴NQ=![]() a,QM=
a,QM=![]() a,
a,
∴BN:NQ:QM=a:![]() a:
a:![]() a=5:3:2.
a=5:3:2.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】(1)在某次考试中,现有甲、乙、丙3名同学,共四科测试实际成绩如下表:(单位:分)
语文 | 数学 | 英语 | 科学 | |
甲 | 95 | 95 | 80 | 150 |
乙 | 105 | 90 | 90 | 139 |
丙 | 100 | 100 | 85 | 139 |
若欲从中表扬2人,请你从平均数的角度分析,那两人将被表扬?
(2)为了提现科学差异,参与测试的语文、数学、英语、科学实际成绩须以2:3:2:3的比例计入折合平均数,请你从折合平均数的角度分析,哪两人将被表扬?