题目内容
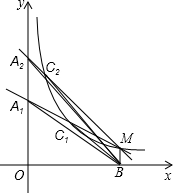 (2012•宁德)如图,点M是反比例函数y=
(2012•宁德)如图,点M是反比例函数y=| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 255 |
| 512 |
| 255 |
| 512 |
分析:根据点M是反比例函数y=
在第一象限内图象上的点,即可得出S△A1BM=
OB×MB=
,再利用C1到BM的距离为A1到BM的距离的一半,得出S1=S△BMC1=
S△A1BM=
,同理即可得出S2=S△A2C2B=
S△BMA2=
,S3=
,S4=
…进而求出S1+S2+S3+…+S8的值即可.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
解答: 解:过点M作MD⊥y轴于点D,过点A1作A1E⊥BM于点E,过点C1作C1F⊥BM于点F,
解:过点M作MD⊥y轴于点D,过点A1作A1E⊥BM于点E,过点C1作C1F⊥BM于点F,
∵点M是反比例函数y=
在第一象限内图象上的点,
∴OB×BM=1,
∴S△A1BM=
OB×MB=
,
∵A1C1=
A1M,即C1为A1M中点,
∴C1到BM的距离C1F为A1到BM的距离A1E的一半,
∴S1=S△BMC1=
S△A1BM=
,
∴S△BMA2=
BM•A2到BM距离=
×BM×BO=
,
∵A2C2=
A2M,
∴C2到BM的距离为A2到BM的距离的
,
∴S2=S△A2C2B=
S△BMA2=
,
同理可得:S3=
,S4=
…
∴
+
+…+
+
,
=
+
+…+
+
,
=
,
故答案为:
.
 解:过点M作MD⊥y轴于点D,过点A1作A1E⊥BM于点E,过点C1作C1F⊥BM于点F,
解:过点M作MD⊥y轴于点D,过点A1作A1E⊥BM于点E,过点C1作C1F⊥BM于点F,∵点M是反比例函数y=
| 1 |
| x |
∴OB×BM=1,
∴S△A1BM=
| 1 |
| 2 |
| 1 |
| 2 |
∵A1C1=
| 1 |
| 2 |
∴C1到BM的距离C1F为A1到BM的距离A1E的一半,
∴S1=S△BMC1=
| 1 |
| 2 |
| 1 |
| 4 |
∴S△BMA2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵A2C2=
| 1 |
| 4 |
∴C2到BM的距离为A2到BM的距离的
| 3 |
| 4 |
∴S2=S△A2C2B=
| 1 |
| 4 |
| 1 |
| 8 |
同理可得:S3=
| 1 |
| 16 |
| 1 |
| 32 |
∴
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 28 |
| 1 |
| 29 |
=
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 256 |
| 1 |
| 512 |
=
| 255 |
| 512 |
故答案为:
| 255 |
| 512 |
点评:此题主要考查了反比例函数的综合应用以及三角形面积关系,根据同底三角形对应高的关系得出面积关系是解题关键.

练习册系列答案
相关题目
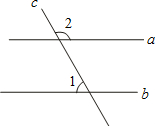 (2012•宁德)如图,直线a∥b,∠1=60°,则∠2=
(2012•宁德)如图,直线a∥b,∠1=60°,则∠2=
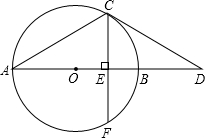 (2012•宁德)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠D=30°.
(2012•宁德)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠D=30°.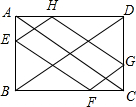 (2012•宁德)如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )
(2012•宁德)如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )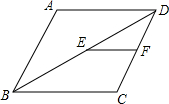 (2012•宁德)如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则AB=
(2012•宁德)如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则AB=