题目内容
 (2012•宁德)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠D=30°.
(2012•宁德)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠D=30°.(1)求∠A的度数;
(2)过点C作CF⊥AB,垂足为E,交⊙O于点F,CF=4
| 3 |
分析:(1)连接OC.利用切线的性质推知△OCD为直角三角形,然后在Rt△OCD中由直角三角形的性质求得圆心角∠COB=60°;最后由圆周角定理求得∠A的度数即可;
(2)利用垂径定理、特殊角的三角函数值求得⊙O的半径OC=4;然后根据弧长的计算公式
来求弧BC的长度.
(2)利用垂径定理、特殊角的三角函数值求得⊙O的半径OC=4;然后根据弧长的计算公式
| nπr |
| 180 |
解答: 解:(1)连接OC.
解:(1)连接OC.
∵CD是⊙O的切线,
∴OC⊥CD,即∠OCD=90°;
又∵∠D=30°,
∴∠COD=60°,即∠COB=60°(直角三角形的两个锐角互余),
∴∠A=
∠COD=30°(同弧所对的圆周角是圆心角的一半);
(2)∵AB是⊙O的直径,CF⊥AB,CF=4
,
∴CE=
CF=2
(垂径定理);
由(1)知,∠COB=60°,
∴OC=
=4,
∴弧BC的长度为:
=
.
 解:(1)连接OC.
解:(1)连接OC.∵CD是⊙O的切线,
∴OC⊥CD,即∠OCD=90°;
又∵∠D=30°,
∴∠COD=60°,即∠COB=60°(直角三角形的两个锐角互余),
∴∠A=
| 1 |
| 2 |
(2)∵AB是⊙O的直径,CF⊥AB,CF=4
| 3 |
∴CE=
| 1 |
| 2 |
| 3 |
由(1)知,∠COB=60°,
∴OC=
| CE |
| sin∠COB |
∴弧BC的长度为:
| 60×π×4 |
| 180 |
| 4π |
| 3 |
点评:本题考查了圆的综合题:同弧所对的圆周角是圆心角的一半;垂直于弦的直径平分弦;运用正弦的定义进行几何计算.

练习册系列答案
相关题目
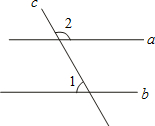 (2012•宁德)如图,直线a∥b,∠1=60°,则∠2=
(2012•宁德)如图,直线a∥b,∠1=60°,则∠2=
 (2012•宁德)如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( )
(2012•宁德)如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥AC∥HG,EH∥BD∥FG,则四边形EFGH的周长是( ) (2012•宁德)如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则AB=
(2012•宁德)如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则AB=