ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘Ύ―ßœΑΓΕ2Θ°1‘≤ΓΖ ±Θ§–ΓΟς”ωΒΫΝΥ’β―υ“ΜΗωΈ ΧβΘΚ»γΆΦΘ®1Θ©ΓΔΘ®2Θ©Υυ ΨΘ§ΓςABCΚΆΓςDBC÷–Θ§ΓœAΘΫΓœDΘΫ90ΓψΘ° ‘÷ΛΟςAΓΔBΓΔCΓΔDΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ°
–ΓΟςœκΒΫΝΥ»γœ¬÷ΛΖ®ΘΚ‘ΎΆΦΘ®1Θ©ΓΔΘ®2Θ©÷–»ΓBC÷–ΒψMΘ§Ν§ΫαAMΓΔDMΘ°‘ρ”–AMΘΫBMΘΫCMΦΑDMΘΫBMΘΫCMΘ§Φ¥AMΘΫBMΘΫCMΘΫDMΘ§Υυ“‘AΓΔBΓΔCΓΔDΥΡΒψ‘Ύ“‘MΈΣ‘≤–ΡΘ§MBΈΣΑκΨΕΒΡ‘≤…œΘ°



ΗυΨί“‘…œΧΫΨΩΈ ΧβΒΟ≥ωΒΡΫα¬έΘ§ΫβΨωœ¬Ν–Έ ΧβΘΚ
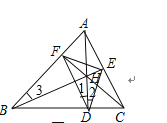
Θ®1Θ©»γΆΦΘ®3Θ©Θ§‘ΎΓςABC÷–Θ§»ΐΧθΗΏADΓΔBEΓΔCFœύΫΜ”ΎΒψHΘ§Ν§ΫαDEΓΔDFΘ§»τΓœBACΘΫ64ΓψΘ§‘ρΓœEDFΘΫ__________ΓψΘ°
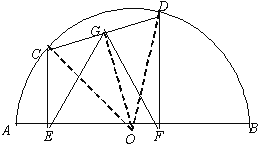
Θ®2Θ©»γΆΦΘ®4Θ©Θ§“―÷ΣAB «Γ―OΒΡ÷±ΨΕΘ§CD «Γ―OΒΡœ“Θ§GΈΣCDΒΡ÷–ΒψΘ§CEΓΆAB”ΎEΘ§DFΓΆAB”ΎFΘ®EΓΔF≤Μ÷ΊΚœΘ©Θ°»τΓœEGFΘΫ60ΓψΘ§«σ÷ΛΘΚCDΘΫ![]() ABΘ°
ABΘ°

ΓΨ¥πΑΗΓΩ52Γψ
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ ![]() ”…(2)“ΉΒΟΘ§Βψ
”…(2)“ΉΒΟΘ§Βψ![]() ‘ΎΆ§“Μ‘≤…œΘ§ΓύΓœ1=Γœ3.
‘ΎΆ§“Μ‘≤…œΘ§ΓύΓœ1=Γœ3.
”…(2)Ά§άμΩ…ΒΟΘ§Βψ![]() ‘ΎΆ§“Μ‘≤…œΘ§ΓύΓœEDH=ΓœECH. Ω…“‘÷ΛΒΟΓœ2=Γœ3Θ§
‘ΎΆ§“Μ‘≤…œΘ§ΓύΓœEDH=ΓœECH. Ω…“‘÷ΛΒΟΓœ2=Γœ3Θ§
«σΒΟΓœEDFΒΡΕ» ΐ.
![]() άϊ”ΟΧΫΨΩΒΟ≥ω
άϊ”ΟΧΫΨΩΒΟ≥ω![]() ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§«“
ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§«“![]() ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§
ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§
ΓœOGEΘΫΓœOCEΘ§ΓœOGFΘΫΓœODFΘ° ΓœOCEΘΪΓœODFΘΫΓœOGEΘΪΓœOGFΘΫΓœEGFΘΫ60ΓψΘ§
Ϋχ“Μ≤Ϋ÷ΛΟςΓςCOD «Β»±Ώ»ΐΫ«–ΈΘ°¥”ΕχΒΟ÷Λ.
‘ΧβΫβΈωΘΚ ![]() »γΆΦΘ§
»γΆΦΘ§
‘ΎΥΡ±Ώ–ΈFBDH÷–, ![]()
”…(2)“ΉΒΟΘ§Βψ![]() ‘ΎΆ§“Μ‘≤…œΘ§
‘ΎΆ§“Μ‘≤…œΘ§
![]()
‘ΎΥΡ±Ώ–Έ![]() ÷–,
÷–, ![]()
”…(2)Ά§άμΩ…ΒΟΘ§Βψ![]() ‘ΎΆ§“Μ‘≤…œΘ§
‘ΎΆ§“Μ‘≤…œΘ§
![]()
![]() «“
«“![]()
![]()
![]()
![]()
![]()
ΓœEDFΘΫ52ΓψΘ°
![]() ÷ΛΟςΘΚΝ§ΫαOCΘ§ODΘ§OGΘ°
÷ΛΟςΘΚΝ§ΫαOCΘ§ODΘ§OGΘ°
ΓΏOCΘΫODΘ§GΈΣCDΒΡ÷–ΒψΘ§ΓύOGΓΆCDΘ°
![]()
![]() «“
«“![]()
![]() ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§«“
ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§«“![]() ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§
ΥΡΒψ‘ΎΆ§“Μ‘≤…œΘ§
ΓύΓœOGEΘΫΓœOCEΘ§ΓœOGFΘΫΓœODFΘ°
ΓύΓœOCEΘΪΓœODFΘΫΓœOGEΘΪΓœOGFΘΫΓœEGFΘΫ60ΓψΘ§
‘ΎRtΓςCEOΚΆ‘ΎRtΓςDFO÷–Θ§
![]()
![]()
![]()
”÷![]()
![]() «Β»±Ώ»ΐΫ«–ΈΘ°
«Β»±Ώ»ΐΫ«–ΈΘ°
![]()
Φ¥![]()

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ