Question

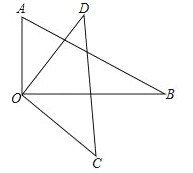
【题目】如图，将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起．

（1）若∠BOD=35°，则∠AOC= ；

（2）若∠AOC=135°，则∠BOD= ；

（3）猜想∠AOC与∠BOD的数量关系，并说明理由．

Answer 1

【答案】（1）145°；（2）45°；（3）∠AOC与∠BOD互补．

【解析】试题分析：（1）先根据∠AOD＝∠AOB－∠BOD计算出∠AOD，然后再根据∠AOC＝∠COD＋∠AOD计算即可；

（2）先根据∠AOD＝∠AOC－∠COD计算出∠AOD，然后再根据∠BOD＝∠AOB－∠AOD计算即可；

（3）先根据（1）（2）的结论猜测出∠AOC与∠BOD互补，将∠AOC拆成∠AOD＋∠BOD＋∠BOC，然后与∠BOD相加即可得出结论．

试题解析：

解：（1）∠AOD＝∠AOB－∠BOD＝90°－35°＝55°，

∴∠AOC＝∠COD＋∠AOD＝90°＋55°＝145°；

（2）∠AOD＝∠AOC－∠COD＝135°－90°＝45°，

∴∠BOD＝∠AOB－∠AOD＝90°－45°＝45°；

（3）∠AOC与∠BOD互补．理由如下：

∠AOC＋∠BOD＝∠AOD＋∠BOD＋∠BOC＋∠BOD

＝(∠AOD＋∠BOD)＋(∠BOC＋∠BOD)

＝∠AOB＋∠COD

＝90°＋90°

＝180°，

即∠AOC与∠BOD互补．