题目内容
已知2011个整数a1、a2、a3、…、a2012满足下列条件:a1=0,a2=-|a1+2|,a3=-|a2+2|,…,a2012=-|a2011+2|,则a1+a2+a3+…+a2012=
- A.0
- B.2012
- C.-2010
- D.-2012
D
分析:根据题意求出a1,a2,a3,a4的值,找出变化规律,然后进行计算即可得解.
解答:a1=0,
a2=-|a1+2|=-|0+2|=-2,
a3=-|a2+2|=-|-2+2|=0,
a4=-|a3+2|=-|0+2|=-2,
…,
所以,第奇数个数是0,第偶数个数是-2,
a1+a2+a3+…+a2012=0+(-2)+0+(-2)+…+(-2)=-2× =-2012.
=-2012.
故选D.
点评:本题是对数字变化规律的考查,求出前几个数得出第奇数个数是0,第偶数个数是-2是解题的关键.
分析:根据题意求出a1,a2,a3,a4的值,找出变化规律,然后进行计算即可得解.
解答:a1=0,
a2=-|a1+2|=-|0+2|=-2,
a3=-|a2+2|=-|-2+2|=0,
a4=-|a3+2|=-|0+2|=-2,
…,
所以,第奇数个数是0,第偶数个数是-2,
a1+a2+a3+…+a2012=0+(-2)+0+(-2)+…+(-2)=-2×
 =-2012.
=-2012.故选D.
点评:本题是对数字变化规律的考查,求出前几个数得出第奇数个数是0,第偶数个数是-2是解题的关键.

练习册系列答案
相关题目
已知2011个整数 、
、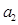 、
、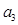 、…、
、…、 满足下列条件:
满足下列条件: ,
, ,
,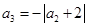 ,…,
,…,
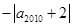 ,则
,则 …
… =
=
 、
、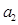 、
、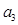 、…、
、…、 满足下列条件:
满足下列条件: ,
, ,
,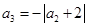 ,…,
,…,
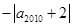 ,则
,则 …
… =
=| A.0 | B.2010 | C.-2010 | D.2011B |
 ,则
,则 、
、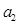 、
、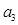 、…、
、…、 满足下列条件:
满足下列条件: ,
,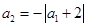 ,
, ,…,
,…,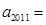
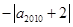 ,则
,则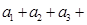 …
…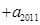 =
=