Question

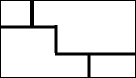
（2013•岳阳）某校有一露天舞台，纵断面如图所示，AC垂直于地面，AB表示楼梯，AE为舞台面，楼梯的坡角∠ABC=45°，坡长AB=2m，为保障安全，学校决定对该楼梯进行改造，降低坡度，拟修新楼梯AD，使∠ADC=30°．
（1）求舞台的高AC（结果保留根号）；
（2）在楼梯口B左侧正前方距离舞台底部C点3m处有一株大树，修新楼梯AD时底端D是否会触到大树？并说明理由．

Answer 1

分析：（1）首先由已知AB=6m，∠ABC=45°求出AC和BC，再由∠ADC=30°求出AD=2AC；
（2）根据勾股定理求出CD后与3m比较后即可得到答案．

解答：解：（1）已知AB=2m，∠ABC=45°，
∴AC=BC=AB•sin45°=2×

2

2

=

2

，
答：舞台的高为

2

米；

（2）已知∠ADC=30°．
∴AD=2AC=2

2

．
CD=AD•cos30°=2

2

×

3

2

=

6

＜3
答：修新楼梯AD时底端D不会触到大树．

点评：此题考查的是解直角三角形的应用，关键是运用锐角三角形函数求解．