题目内容
如图①,若二次函数y=
x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y=
x的图象的对称点为C.
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y=
x的图象于点D,连结AC,交正比例函数y=
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.

| ||
| 6 |
| 3 |
(1)求b、c的值;
(2)证明:点C在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数y=
| 3 |
| 3 |

(1)∵点A(-2,0),B(3,0)在抛物线y=
x2+bx+c上,
∴
,
解得:b=-
,c=-
.
(2)设点F在直线y=
x上,且F(2,2
).
如答图1所示,过点F作FH⊥x轴于点H,则FH=2
,OH=2,
∴tan∠FOB=
=
,∴∠FOB=60°.
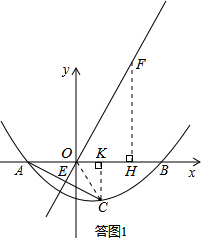
∴∠AOE=∠FOB=60°.
连接OC,过点C作CK⊥x轴于点K.
∵点A、C关于y=
x对称,∴OC=OA=2,∠COE=∠AOE=60°.
∴∠COK=180°-∠AOE-∠COE=60°.
在Rt△COK中,CK=OC•sin60°=2×
=
,OK=OC•cos60°=2×
=1.
∴C(1,-
).
抛物线的解析式为:y=
x2-
x-
,当x=1时,y=-
,
∴点C在所求二次函数的图象上.
(3)假设存在.
如答图1所示,在Rt△ACK中,由勾股定理得:AC=
=
=2
.
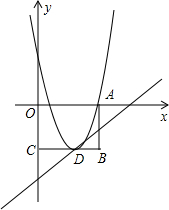
如答图2所示,∵OB=3,∴BD=3
,AB=OA+OB=5.
在Rt△ABD中,由勾股定理得:AD=
=
=2
.
∵点A、C关于y=
x对称,
∴CD=AD=2
,∠DAC=∠DCA,AE=CE=
AC=
.
连接PQ、PE,QE,则∠APE=∠QPE,∠PQE=∠CQE.

在四边形APQC中,∠DAC+∠APQ+∠PQC+∠DCA=360°(四边形内角和等于360°),
即2∠DAC+2∠APE+2∠CQE=360°,
∴∠DAC+∠APE+∠CQE=180°.
又∵∠DAC+∠APE+∠AEP=180°(三角形内角和定理),
∴∠AEP=∠CQE.
在△APE与△CEQ中,∵∠DAC=∠DCA,∠AEP=∠CQE,
∴△APE∽△CEQ,
∴
=
,即:
=
,
整理得:2t2-4
t+3=0,
解得:t=
或t=
(t<
,所以舍去)
∴存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,此时t=
.
| ||
| 6 |
∴
|
解得:b=-
| ||
| 6 |
| 3 |
(2)设点F在直线y=
| 3 |
| 3 |
如答图1所示,过点F作FH⊥x轴于点H,则FH=2
| 3 |
∴tan∠FOB=
| FH |
| OH |
| 3 |

∴∠AOE=∠FOB=60°.
连接OC,过点C作CK⊥x轴于点K.
∵点A、C关于y=
| 3 |
∴∠COK=180°-∠AOE-∠COE=60°.
在Rt△COK中,CK=OC•sin60°=2×
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴C(1,-
| 3 |
抛物线的解析式为:y=
| ||
| 6 |
| ||
| 6 |
| 3 |
| 3 |
∴点C在所求二次函数的图象上.
(3)假设存在.
如答图1所示,在Rt△ACK中,由勾股定理得:AC=
| AK2+CK2 |
32+(
|
| 3 |
如答图2所示,∵OB=3,∴BD=3
| 3 |
在Rt△ABD中,由勾股定理得:AD=
| AB2+BD2 |
52+(3
|
| 13 |
∵点A、C关于y=
| 3 |
∴CD=AD=2
| 13 |
| 1 |
| 2 |
| 3 |
连接PQ、PE,QE,则∠APE=∠QPE,∠PQE=∠CQE.

在四边形APQC中,∠DAC+∠APQ+∠PQC+∠DCA=360°(四边形内角和等于360°),
即2∠DAC+2∠APE+2∠CQE=360°,
∴∠DAC+∠APE+∠CQE=180°.
又∵∠DAC+∠APE+∠AEP=180°(三角形内角和定理),
∴∠AEP=∠CQE.
在△APE与△CEQ中,∵∠DAC=∠DCA,∠AEP=∠CQE,
∴△APE∽△CEQ,
∴
| CQ |
| AE |
| CE |
| AP |
2
| ||
|
| ||
| 2t |
整理得:2t2-4
| 13 |
解得:t=
2
| ||||
| 2 |
2
| ||||
| 2 |
| 13 |
∴存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,此时t=
2
| ||||
| 2 |

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目


 别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:
别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:
 B运动;同时,点N从B点出发沿折线段BC-CO以每秒1个单位长的速度向终点O运动、设运动时间为t秒.
B运动;同时,点N从B点出发沿折线段BC-CO以每秒1个单位长的速度向终点O运动、设运动时间为t秒.