题目内容
某航船以30海里/时的速度向正北方向航行,在A处看灯塔Q在航船北偏东30°处,半小时后航行到B处,此时灯塔Q与航船的距离最短.(1)请你在图中画出点B的位置;
(2)求灯塔Q到B处的距离.(精确到0.1海里)
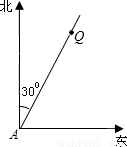
【答案】分析:(1)根据“垂线段最短”可知,从Q向AN作垂线,垂足即为B点;
(2)根据航船的速度求出AB的值,再由锐角三角函数的定义即可求出BQ的长.
解答:解:(1)∵“垂线段最短”,
∴从Q向AN作垂线,垂足即为B点,
如图所示:
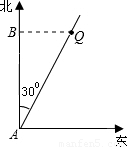
(2)∵航船以30海里/时的速度向正北方向航行,半小时后航行到B处,
∴AB=15海里,
∴BQ=ABtan∠BAQ=15×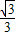 =5
=5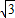 ≈5×1.73=8.65≈8.7(海里).
≈5×1.73=8.65≈8.7(海里).
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
(2)根据航船的速度求出AB的值,再由锐角三角函数的定义即可求出BQ的长.
解答:解:(1)∵“垂线段最短”,
∴从Q向AN作垂线,垂足即为B点,
如图所示:

(2)∵航船以30海里/时的速度向正北方向航行,半小时后航行到B处,
∴AB=15海里,
∴BQ=ABtan∠BAQ=15×
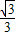 =5
=5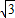 ≈5×1.73=8.65≈8.7(海里).
≈5×1.73=8.65≈8.7(海里).点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 灯塔Q与航船的距离最短.
灯塔Q与航船的距离最短.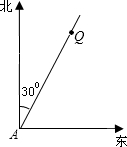 灯塔Q与航船的距离最短.
灯塔Q与航船的距离最短.