Question

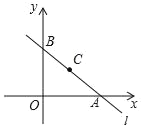
【题目】在平面直角坐标系xOy中，直线l与x轴，y轴分别交于A、B两点，且过点B（0，4）和C（2，2）两点．

（1）求直线l的解析式；

（2）求△AOB的面积；

（3）点P是x轴上一点，且满足△ABP为等腰三角形，直接写出所有满足条件的点P的坐标．

Answer 1

【答案】（1）y＝﹣x+4；（2）8；（3）点P坐标为（﹣4，0）或（4+4，0）或（4﹣4，0）或（0，0）

【解析】

（1）直线过（2，2）和（0，4）两点，则 待定系数法求解析式．

（2）先求A点坐标，即可求△AOB的面积

（3）分三类讨论，可求点P的坐标

解（1）设直线l的解析式y＝kx+b

∵直线过（2，2）和（0，4）

∴

解得：

∴直线l的解析式y＝﹣x+4

（2）令y＝0，则x＝4

∴A（4，0）

∴S△AOB＝×AO×BO＝×4×4＝8

（3）∵OA＝4，OB＝4

∴AB＝4

若AB＝AP＝4

∴在点A左边，OP＝4﹣4，

在点A右边，OP＝4+4

∴点P坐标（4+4，0），（4﹣4，0）

若BP＝BP＝4

∴P（﹣4，0）

若AP＝BP则点P在AB的垂直平分线上，

∵△AOB是等腰直角三角形，

∴AB的垂直平分线过点O

∴点P坐标（0，0）