题目内容
甲、乙两车分别从A地将一批物品运往B地,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的数据回答:
(1)甲车出发多长时间后被乙车追上?
(2)甲车与乙车在距离A地多远处迎面相遇?
(3)甲车从B地返回的速度多大时,才能比乙车先回到A地?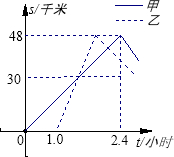
(1)1.5小时;(2)40.8;(3)48千米/小时.
解析试题分析:(1)由图知,可设甲车由A地前往B地的函数解析式为s=kt,把将(2.4,48)代入即可求出此一次函数的表达式,再根据图中S=30即可求出t的值;
(2)可设乙车由A地前往B地函数的解析式为s=pt+m,将(1.0,0)和(1.5,30)代入即可求出此表达式,进而可求出t的值,同理设乙车由B地返回A地的函数的解析式为s=-30t+n,把将(1.8,48)代入即可求解;
(3)求出乙车返回到A地时所需的时间及乙车的速度即可.
(1)由图知,可设甲车由A地前往B地的函数解析式为s=kt,
将(2.4,48)代入,解得k=20,所以s=20t,
由图可知,在距A地30千米处,乙车追上甲车,所以当s=30千米时,t=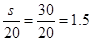 (小时).
(小时).
即甲车出发1.5小时后被乙车追上,
(2)由图知,可设乙车由A地前往B地函数的解析式为s=pt+m,
将(1.0,0)和(1.5,30)代入,得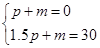 ,解得
,解得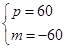 ,
,
所以s=60t-60,当乙车到达B地时,s=48千米.代入s=60t-60,得t=1.8小时,
又设乙车由B地返回A地的函数的解析式为s=-30t+n,
将(1.8,48)代入,得48=-30×1.8+n,解得n=102,
所以s=-30t+102,当甲车与乙车迎面相遇时,有-30t+102=20t
解得t=2.04小时代入s=20t,得s=40.8千米,即甲车与乙车在距离A地40.8千米处迎面相遇;
(3)当乙车返回到A地时,有-30t+102=0,解得t=3.4小时,
甲车要比乙车先回到A地,速度应大于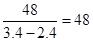 (千米/小时).
(千米/小时).
考点:一次函数的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案我市某工艺厂为配合奥运会,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
| 销售单价x(元/件) | …… | 30 | 40 | 50 | 60 | …… |
| 每天销售量y(件) | …… | 500 | 400 | 300 | 200 | …… |

(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
 x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动. 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.
 (x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
(x > 0,k是常数)的图象经过点A(1,4),点B(m , n),其中m>1, AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
 与一次函数
与一次函数 的图象交于A(3,1)、B(m,-3)两点.
的图象交于A(3,1)、B(m,-3)两点. OA,请直接写出点P的坐标.
OA,请直接写出点P的坐标.