题目内容
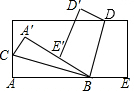
如图长方形ABCD,E是AD的中点,将△ABE沿BE折叠后的△GBE,且点G在长方形ABCD内部,延长BG交DC于F,
(1)求证:GF=DF;
(2)若DC=2DF,求
的值;
(3)若DC=nDF,且
=
,则n=______.
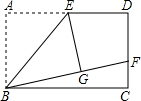
(1)求证:GF=DF;
(2)若DC=2DF,求
| AD |
| AB |
(3)若DC=nDF,且
| AD |
| AB |
2
| ||
| 3 |

(1)证明:连接EF,
∵△BGE由△BAE翻折而成,
∴∠A=∠EGB=90°,AE=EG,
∵E是AD的中点,
∴AE=EG=DE,
∴
∴Rt△EGF≌Rt△EDF,
∴GF=DF;
(2)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=2DF,
∴CF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x;
在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2
∴y=2
x,
∴
=
=
;
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=n•DF,
∴BF=BG+GF=(n+1)x
在Rt△BCF中,BC2+CF2=BF2,即y2+[(n-1)x]2=[(n+1)x]2
∴y=2x
,
∴
=
=
,
∵
=
,
∴n=3.
故答案为:3.

∵△BGE由△BAE翻折而成,
∴∠A=∠EGB=90°,AE=EG,
∵E是AD的中点,
∴AE=EG=DE,
∴
|
∴Rt△EGF≌Rt△EDF,
∴GF=DF;
(2)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=2DF,
∴CF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x;
在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2
∴y=2
| 2 |
∴
| AD |
| AB |
| y |
| 2x |
| 2 |
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=n•DF,
∴BF=BG+GF=(n+1)x
在Rt△BCF中,BC2+CF2=BF2,即y2+[(n-1)x]2=[(n+1)x]2
∴y=2x
| n |
∴
| AD |
| AB |
| y |
| nx |
2
| ||
| n |
∵
| AD |
| AB |
2
| ||
| 3 |
∴n=3.
故答案为:3.


练习册系列答案
相关题目
 对称的△A2 B2C2,其中点A、B、C的对应点分别为点A2、B2、C2,并写出点A2的坐标.
对称的△A2 B2C2,其中点A、B、C的对应点分别为点A2、B2、C2,并写出点A2的坐标.