题目内容
在△ABC中,已知BC=4cm,∠BAC=45°,则△ABC的最大面积是( )
| A、8cm2 | ||
| B、16cm2 | ||
C、4(1+
| ||
D、8(1+
|
分析:作出△ABC的外接圆⊙O,连接OB、OC,根据同弧所对的圆周角等于圆心角的一半求出∠BOC=90°,过点O作OD⊥BC,根据等腰直角三角形的性质求出半径OB的长度,再根据三角形的面积公式,底边BC一定,边BC上的高越大则三角形的面积越大,所以,当BC边上的高过圆心O时,三角形的面积最大,进行求解即可.
解答: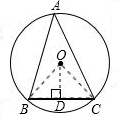 解:如图,△ABC的外接圆⊙O,连接OB、OC,
解:如图,△ABC的外接圆⊙O,连接OB、OC,
∵∠BAC=45°,
∴∠BOC=2∠BAC=2×45°=90°,
过点O作OD⊥BC,垂足为D,则
BD=CD=
BC=2(等腰三角形三线合一),
∵∠BOC=90°,OD⊥BC,
∴OD=
BC=2,
半径OB=
=
=2
,
∵BC=4cm一定,
∴BC边上的高越大,则△ABC的面积越大,当高过圆心时,最大,
此时BC边上的高为:2
+2,
∴△ABC的最大面积是:
×4×(2
+2)=4(
+1)cm2.
故选C.
 解:如图,△ABC的外接圆⊙O,连接OB、OC,
解:如图,△ABC的外接圆⊙O,连接OB、OC,∵∠BAC=45°,
∴∠BOC=2∠BAC=2×45°=90°,
过点O作OD⊥BC,垂足为D,则
BD=CD=
| 1 |
| 2 |
∵∠BOC=90°,OD⊥BC,
∴OD=
| 1 |
| 2 |
半径OB=
| OD2+BD2 |
| 22+22 |
| 2 |
∵BC=4cm一定,
∴BC边上的高越大,则△ABC的面积越大,当高过圆心时,最大,
此时BC边上的高为:2
| 2 |
∴△ABC的最大面积是:
| 1 |
| 2 |
| 2 |
| 2 |
故选C.
点评:本题考查了圆周角定理,垂径定理的应用,以及三角形的面积公式,根据题意作出△ABC的外接圆,利用圆的知识进行求解是解题的关键,本题灵活性较强,是道好题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
