题目内容
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,(1)若CD=16,BE=4,则⊙O的半径为___;(2)点M在⊙O上,MD恰好经过圆心O,连接MB,若∠M=∠D,则∠D的度数为__.
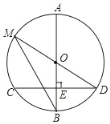
【答案】(1)10; (2)30°.
【解析】
(1)设⊙O的半径为r,则OE=r﹣4,由垂径定理求得DE=EC=![]() CD=8,在Rt△OED中,根据勾股定理可得r2=(r﹣4)2+82,解方程求得r的值即可;(2)由圆周角定理可得∠DOE=2∠M,由∠M=∠D,可得∠DOE=2∠D,再Rt△OED中,即可求得∠D=30°.
CD=8,在Rt△OED中,根据勾股定理可得r2=(r﹣4)2+82,解方程求得r的值即可;(2)由圆周角定理可得∠DOE=2∠M,由∠M=∠D,可得∠DOE=2∠D,再Rt△OED中,即可求得∠D=30°.
(1)设⊙O的半径为r,则OE=r﹣4,
∵AB是⊙O的直径,弦CD⊥AB,
∴DE=EC=![]() CD=8,
CD=8,
在Rt△OED中,OD2=OE2+DE2,即r2=(r﹣4)2+82,
解得,r=10,
故答案为:10;
(2)由圆周角定理得,∠DOE=2∠M,
∵∠M=∠D,
∴∠DOE=2∠D,
∴∠D=30°,
故答案为:30°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目