Question

已知抛物线y=-x²+kx-k+2．
（1）求证：无论k为任何实数，该抛物线与x轴都有两个交点；
（2）在抛物线上有一点P（m，n），n＜0，OP=

10

3

，且线段OP与x轴正半轴所夹锐角的正弦值为

4

5

，求该抛物线的解析式；
（3）将（2）中的抛物线x轴上方的部分沿x轴翻折，与原图象的另一部分组成一个新的图形M，当直线y=-x+b与图形M有四个交点时，求b的取值范围．

Answer 1

分析：（1）先令y=0可得出关于x的一元二次方程，再根据一元二次方程的解与判别式△的关系即可得出结论；
（2）过点P作PA⊥x轴于A，则∠OAP=90°，由OP=

10

3

，sin∠POA=

4

5

，可得出AP，OA的长，再根据n＜0，可得出P点坐标，把P点坐标代入抛物线y=-x²+kx-k+2即可得出k的值，故可得出抛物线解析式；
（3））由（2）中求出的抛物线的解析式可令y=0求出x的值，故可得出抛物线与x轴的交点坐标，求出直线y=-x+b经过点B时b的值，再求出直线与抛物线相切时b的值即可得出b的取值范围．

解答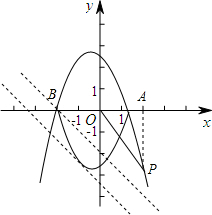：（1）证明：当y=0时，得x²-kx+k-2=0．
∵b²-4ac=k²-4（k-2）=（k-2）²+4．
∵（k-2）²≥0，
∴（k-2）²+4＞0．
∴无论k为任何实数，该抛物线与x轴都有两个交点；

（2）解：如图，过点P作PA⊥x轴于A，则∠OAP=90°，
∵OP=

10

3

，sin∠POA=

4

5

，
∴AP=

8

3

，OA=2，
∵n＜0，
∴P（2，-

8

3

），
∵P在抛物线上，
∴-

8

3

=-4+2k-k+2，
∴k=-

2

3

，
∴抛物线解析式为y=-x²-

2

3

x+

8

3

；

（3）解：∵当y=0时，-x²-

2

3

x+

8

3

=0，
∴x₁=-2，x₂=

4

3

，
∴抛物线与x轴相交于点B（-2，0），（

4

3

，0），
∴当直线y=-x+b经过点B（-2，0）时，b=-2．
当直线y=-x+b与抛物线y=-x²-

2

3

x+

8

3

相切时，x²+

2

3

x-

8

3

=-x+b，
∴△=

25

9

+4（b+

8

3

）=0．
∴b=-

121

36

．
∴当-

121

36

＜b＜-2时，直线与图形M有四个交点．

点评：本题考查的是二次函数综合题，涉及到直线与抛物线的交点问题、用待定系数法求一次函数及二次函数的解析式等知识，难度适中．